Moskva, Moscow, Russian Federation
Moskva, Moscow, Russian Federation
Since ancient times, people interested in the study of the world around them, including forms. From what appeared geometry – metric description of the Earth, as a science. Since man is essentially a «solver», the special interest of the people causing the problem difficult to resolve or can not be solved at all. Above these objectives mankind can reflect thousands of years. The objectives of this type include «square the circle» formed by more ancient Greek philosopher Plato. By geometric constructions, designed to find a solution, it must meet the following requirements: they must be executed only by means of a ruler and compass, without divisions.
squaring the circle, geometric constructions by ruler and compass, area of a circle, ellipse area.
При решении задач начертательной геометрии, как правило, прибегают к переходу в геометрию на плоскости (планиметрию). Это реализуется, например, при определении натуральной величины отрезка прямой методом прямоугольных треугольников или одним из способов преобразования чертежа (введение вспомогательных плоскостей проекций, вращение вокруг проецирующей оси и пр.). В журнале «Геометрия и графика» уделяется большое внимание решению задач начертательной геометрии и развитию науки в целом [4-10]. При этом для решения ряда задач может оказаться необходимой оценка площадей различных плоских фигур. Под методами определения площади в данной статье подразумевается графические построения, позволяющие с той или иной точностью, достижимой на данный момент, определить величины сторон квадрата или прямоугольника с площадью, равной описываемой какой-либо заданной замкнутой линией. В данном случае в качестве таких линий рассмотрены замкнутые коники - окружность и эллипс. Известно, что ряд подобных задач не имеют точного решения, но при этом, как оказывается, на практике можно добиться точного результата, вполне удовлетворяющего требованиям к выполнению, например, графических, землемерных, строительных и других работ.
К задачам такого рода можно отнести «квадратуру круга», сформированную еще древнегреческим философом Платоном. К геометрическим построениям, предназначенным для отыскания решения, он предъявлял следующие требования: они должны выполняться лишь с помощью циркуля и линейки без делений. Как стало очевидно значительно позже, в XIX в., такие ограничения к способам решения делают задачу неразрешимой. Это утверждение основывается на доказательстве немецкого математика Линдермана того факта, что число π, определяющее отношение длины окружности к диаметру, трансцендентное, т.е. такое, которое не может служить корнем никакого алгебраического уравнения с целыми коэффициентами [2, 3]. При построениях, необходимых для получения величины стороны квадрата, равновеликого по площади заданному кругу, необходимо иметь возможность оперировать величиной , которая с точностью, необходимой для построений, равна 0,886. Следовательно, точность метода решения задачи зависит от того, насколько близкой к этой величине будет сомножитель, заменяющий ее в формуле
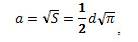 , (1)
, (1)
где a - сторона искомого квадрата; S - площадь заданного круга.
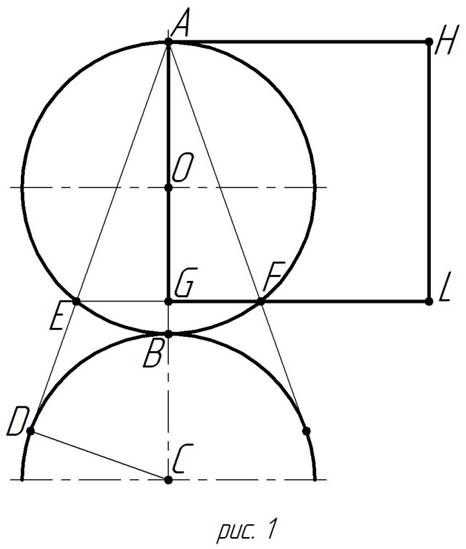
Нам удалось найти решение задачи о «квадратуре круга», сформулированной Платоном с установленными им требованиями, которое дает результат с погрешностью, не превышающей 0,5%, что вполне удовлетворяет общепринятым требованиям к точности выполнения графических работ [1]. Оно состоит в следующем (см. рисунок 1).
С центрами в точках O и C, расположенными на одной оси, строятся, соответственно, заданный круг и касательная к нему дуга окружности того же радиуса. Из наиболее удаленной от центра C точки A круга проводят две касательные к дуге, которые пересекают периметр круга в точках E и F.
На основании продолжения хорды EF и длины отсекаемой ею большей части AG диаметра круга с помощью циркуля находят недостающие вершины L и H искомого квадрата AGLH.
Расчет величины отрезка AG, определяющего сторону искомого квадрата, сводится к использованию подобия пар треугольников ACD и AEB, откуда  и ACD и AEG, откуда AG = 0,(8)d (сравните с
и ACD и AEG, откуда AG = 0,(8)d (сравните с  ), что и дает возможность решить задачу с указанной выше весьма незначительной погрешностью.
), что и дает возможность решить задачу с указанной выше весьма незначительной погрешностью.
Формула площади эллипса S = πRr может быть представлена в виде
 . (2)
. (2)
Корень квадратный из площади (см. каждый из сомножителей последней формулы) - это не что иное, как сторона квадрата, равновеликого по площади кругу, образованному окружностью соответствующего диаметра. Значит, площадь эллипса с полуосями R и r равновелика площади прямоугольника, сторонами a и b которого являются стороны квадратов, равновеликих по площадям круга с радиусом R и r.
Построения, необходимые для определения величин a и b, производятся способом, аналогичным приведенным на рисунке 1, и показаны на рисунке 2. При этом погрешности определений, как указывалось выше, крайне незначительны.

Поскольку окружность представляет собой частный случай проекции эллипса, вращающегося вокруг своей меньшей оси (при ее параллельности плоскости проекций, что видно из рисунка 2), то построения с целью получения величин a и b можно было производить и на эллипсах, что, все же, нецелесообразно.
1. Voloshin-Chelpan, E.K. Priblizhennye metody resheniya zadach o kvadrature kruga i trisekcii ugla [Text] / E.K. Voloshin-CHelpan, N.S. Kadykova, G.F. Kudryavcev // Sb. «Sovremennye problemy geometricheskogo modelirovaniya», Materialy Vtoroj ukrainsko-rossijskoj nauchno-prakticheskoj konferencii. - Har´kov, 2007 - Рр. 260-202.
2. Sal´kov, N.A. Ehllips: kasatel´naya i normal´ [Text] / N.A. Sal´kov // Geometriya i grafika. - 2013. - T. 1. - № 1. - Рр. 35-37.
3. Bermant, A.F. Graficheskij spravochnik po matematike atlas krivyh [Text] / A.F. Bermant. - Moskva, Leningrad: Ob´edinennoe nauchno-tekhnicheskoe izdatel´stvo NKTP SSSR, 1937. - 211 р.
4. Ivanov, G.S. O zadachah nachertatel´noj geometrii s mnimymi resheniyami [Text] / G.S. Ivanov, I.M. Dmitrieva // Geometriya i grafika. - 2015. - T. 3. - № 2. - Рр. 3-8. -DOI:https://doi.org/10.12737/12163.
5. Ivanov, G.S. K vyboru posrednika pri reshenii pervoj pozicionnoj zadachi [Text] / G.S. Ivanov, I.M. Dmitrieva // Geometriya i grafika. - 2015. - T. 3. - № 1. - Рр. 26-30. - DOI:https://doi.org/10.12737/10455.
6. Volkov, V.Yа. Ehlementy matematizacii teoreticheskih osnov nachertatel´noj geometrii [Text] / V.Yа. Volkov [et al.] // Geometriya i grafika. - 2015. - T. 3. - № 1. - Рр. 3-15. - DOI:https://doi.org/10.12737/10453.
7. Ivanov, G.S. Kompetentnostnyj podhod k soderzhaniyu kursa nachertatel´noj geometrii [Text] / G.S. Ivanov // Geometriya i grafika. - 2013. - T. 1. - № 2. - Рр. 3-5. - DOI:https://doi.org/10.12737/775.
8. Sal´kov, N.A. Svojstva ciklid Dyupena i ih primenenie [Text] Chast´ 1 / N.A. Sal´kov // Geometriya i grafika. - 2015. - T. 3. - № 1. - Рр. 16-25. - DOI:https://doi.org/10.12737/10454.
9. Sal´kov, N.A. Svojstva ciklid Dyupena i ih primenenie [Text] Chast´ 2 / N.A. Sal´kov // Geometriya i grafika. - 2015. - T. 3. - № 2. - Рр. 9-22. - DOI:https://doi.org/10.12737/12164.
10. Sal´kov, N.A. Svojstva ciklid Dyupena i ih primenenie [Text] Chast´ 3: sopryazheniya / N.A. Sal´kov // Geometriya i grafika. - 2015. - T. 3. - № 4. - Рр. 3-14. - DOI:https://doi.org/10.12737/17345.






