from 01.10.2008 until now
Russian Federation
This paper describes the application of the method of parametric geometry for modeling of roads. Parametric geometry is the basis of a frame-a parametric method of design of surfaces. In Chapter 1 the elements of a frame-a parametric method of design of surfaces are given. Chapter 2 contains a review of issues relating to the design of the highways currently. Chapter 3 is a geometrical and mathematical modeling of linear and superficial forms of roads. In Chapter 4 the local characteristics of roads on curved areas are given. Chapter 5 is devoted to the development of software is the visualization of linear and superficial forms of roads.
geometry, descriptive geometry, parametric geometry, modeling, roads.
Актуальность изучения инженером геометрии, геометрического моделирования исходит из того, что все существующие материальные предметы имеют свои формы, свои поверхности. При этом геометрия не рассматривает воплощение этих форм в материале, наоборот – она абстрагируется от материального изготовления. Ее методы поэтому являются наиболее общими, и на основе этих методов впоследствии производятся все необходимые расчеты, подбирается материал.
Предметом геометрии вообще, и геометрического моделирования в частности, являются геометрические формы и их отношения. Формирование и изучение пространственных форм – вот чем занимается геометрия.
С геометрией связано понятие эстетики и красоты. Эстетики вообще и технической эстетики в частности. Есть конструкции, форма которых несет функциональное значение: от формы самолета зависит его скорость, грузоподъемность, виражность, высота потолка; форма корабля или подводной лодки влияет на скоростные характеристики; для турбин форма лопаток – единственное, что может увеличить ее мощность; особое место занимает форма космических кораблей.
Моделирование, в том числе и геометрическое, – чисто инженерная работа. Инженер, не овладевший способностью мыслить геометрически, не умеющий оперировать пространственными формами, не сможет овладеть и методами геометрического моделирования. Поэтому к своему геометрическому образованию будущий инженер должен подходить со всей ответственностью. Геометрическая модель каждого объекта является базой для его математической модели, которая, в свою очередь, служит основой для разработки программного обеспечения на компьютере.
Нужно сказать, что у объектов, хоть сколько-нибудь связанных со скоростными характеристиками, форма имеет довлеющее значение. К таким объектам принадлежат и дороги: железные и автомобильные.
В 2012 г. была опубликована монография «Моделирование автомобильных дорог» [13].
В работе рассматривается применение метода параметрической геометрии [14] к моделированию автомобильных дорог.
Параметрическая геометрия является основой каркасно-параметрического метода конструирования поверхностей.
В гл.1 были представлены элементы каркасно-параметрического метода конструирования поверхностей, разработанного акад. Н.Ф. Четверухиным и его учеником проф. Н.Н. Рыжовым и дополненного многочисленными учениками этих выдающихся ученых. В том числе и автором данной статьи.
Первоначально поверхность проектировалась исключительно в виде чертежа. С потребностью увеличить точность конструирования графическая модель стала дополняться аналитической. В настоящее время в связи с повышением роли компьютера в науке и производстве основным носителем информации служит математическая модель, на базе которой и с помощью компьютера в автоматизированном режиме получают чертежи и другую проектную документацию, проводят исследования проектируемой поверхности, обеспечивают ее воспроизводство.
Методы конструирования поверхностей можно разделить на две группы [3]. В первую группу входят методы, при помощи которых поверхность формируется как единая, монофункциональная фигура. Во вторую группу входят методы, когда поверхность формируется как пространственный обвод, состоящий из отсеков нескольких поверхностей, «сшитых» между собой с учетом каких-то накладываемых условий.
Базой для данной работы явились следующие методы.
Кинематический метод конструирования поверхностей [1; 3; 5; 7; 12] предполагает образование поверхности некоторой линией постоянной или переменной формы, перемещающейся в пространстве по определенному закону [2, 4]. Этот метод отличается большой наглядностью и простотой, что и определило его широкое применение в инженерной практике.
В области теории каркаса фундаментальными являются работы профессора Рыжова Н.Н. [8–10 и др.]. Каркасная теория задания и конструирования поверхностей дает общую точку зрения на вопросы геометрического конструирования поверхностей, задания их в пространстве и на чертеже, обобщает различные способы и приемы прикладной геометрии поверхностей. В работах [6, 11] получает развитие идея формализации процесса конструирования поверхностей, как по отдельным вопросам, так и всего метода в целом. Формализация таких вопросов как составление закона каркаса, выявление определителя поверхности, получение линии каркаса как элемента непрерывного каркаса поверхности, является главным моментом в проблеме автоматизации этих процессов.
Конструирование поверхностей получением их каркасов имеет определенные преимущества перед другими традиционными математическими методами, так как в реальных условиях производства поверхность изготавливается не как непрерывное двухпараметрическое множество точек, а как дискретное семейство линий, которое при необходимости сглаживается.
Дискретный каркас с наперед заданной плотностью расположения линий можно получить из заданного непрерывного каркаса. Современные технические средства позволяют получить и воспроизводить дискретные каркасы с плотностью, на несколько порядков превосходящей требуемую в инженерной практике. Это дает возможность при решении инженерных задач пользоваться приближенными методами там, где решение классическими методами анализа по тем или иным причинам затруднено.
Однопараметрическое множество линий, образующее каркас некоторой поверхности, можно получить двумя способами: наложением геометрических условий на элементы многопараметрического множества или размножением первоначально заданной производящей линии путем преобразования пространства. Оба способа получили широкое распространение в прикладной геометрии поверхностей и являются основными при конструировании каркасных поверхностей.
Рассмотрим основные положения, раскрывающие сущность каркасно-параметрического метода.
Наперед заданные требования к конструируемой поверхности предъявляются в виде геометрических условий, каждое из которых выступает или в виде параметра элемента каркаса, или в виде функций, устанавливающих определенную зависимость между параметрами элемента каркаса. Каждое из геометрических условий задает определенное число связей между параметрами элементов каркаса, это число называется параметрическим числом данного условия.
При каркасно-параметрическом методе конструирования поверхностей ∞1 (однопараметрическое множество) линий, представляющих собой каркас поверхности, получается выделением этого множества из ∞е (е-параметрического множества) линий некоторого пространства. Если элемент каркаса в некотором пространстве определен по форме и положению е параметрами (е = р+q, где р – число параметров формы, а q – число параметров положения), то это означает, что все пространство заполнено ∞е этих линий. Задавая 1,2, … , (е-1) параметр, можно из ∞е выделить ∞е-1, ∞е-2, … , ∞1 линий. Оставшийся свободным е-й параметр выступает в качестве параметра каркаса.
К аналогичному результату можно прийти, связывая функционально параметры элемента каркаса αi (i=1,2, … , e) соответственно 1,2, … , (е-1) связью. Такая связь устанавливается заданием геометрических условий, предъявляемых к линии – элементу каркаса. Совокупность геометрических условий, выделяющих линейный каркас из ∞е линий, образует закон каркаса. Поскольку каждое из геометрических условий может иметь различное от других условий параметрическое число, то количество таких условий в законе каркаса должно быть таким, чтобы сумма их параметрических чисел равнялась (е+1).
Геометрические условия, входящие в закон каркаса, несут информацию также и об определителе. Эта информация содержится в виде описания тех геометрических образов, через которые осуществляется связь параметров элементов каркаса.
К аналогичному результату можно прийти, связывая функционально параметры элемента каркаса αi (i=1,2, … , e) соответственно 1,2, … , (е-1) связью. Такая связь устанавливается заданием геометрических условий, предъявляемых к линии – элементу каркаса. Совокупность геометрических условий, выделяющих линейный каркас из ∞е линий, образует закон каркаса. Поскольку каждое из геометрических условий может иметь различное от других условий параметрическое число, то количество таких условий в законе каркаса должно быть таким, чтобы сумма их параметрических чисел равнялась (е+1).
Геометрические условия, входящие в закон каркаса, несут информацию также и об определителе. Эта информация содержится в виде описания тех геометрических образов, через которые осуществляется связь параметров элементов каркаса.
Каркасно-параметрический метод конструирования поверхностей состоит в обобщенном виде из следующих частей:
1. Определение исходного ∞е линий, из которых выделяется каркас.
2. Выбор геометрических условий, обеспечивающих наперед заданные требования.
3. Параметрическая оценка геометрических условий.
4. Составление закона каркаса.
5. Выявление принципиального определителя по закону каркаса.
6. Определение метода получения линии каркаса.
7. Реализация метода получения линии каркаса.
8. Воспроизведение линии в каком-нибудь виде.
Каркасно-параметрический метод задания и конструирования поверхностей позволяет осуществить переход от конструктивно-кинематического задания поверхности к аналитическому.
Все многообразие ∞е кривых пространства можно записать в виде системы
 Ф1(X,Y,Z, α1, α2, … , αe)=0;
Ф1(X,Y,Z, α1, α2, … , αe)=0;
Ф2(X,Y,Z, α1, α2, … , αe)=0, (1)
где αi – параметр элемента каркаса.
Закон каркаса можно выразить системой из (е-1) уравнений
Ψi(α1, α2, … , αe)=0; i=1,2, … , (е-1). (2)
Исключив (е-1) параметр из (е+1) уравнений (1) и (2), получим уравнение каркаса с параметром каркаса αk:
 F1(X,Y,Z, αk)=0;
F1(X,Y,Z, αk)=0;
F2(X,Y,Z, αk)=0. (3)
Исключив параметр каркаса αk, можно получить уравнение поверхности в виде:
F(X,Y,Z)=0. (4)
Таким образом, каркасно-параметрический метод является достаточно универсальным методом прикладной геометрии поверхностей. Метод отличается высокой формализованностью и универсальностью его алгоритмов, что является важным моментом в вопросе автоматизации конструирования поверхностей.
Во вторую группу конструирования поверхностей входят такие методы, как метод Кунса, метод Фергюсона, метод Безье, метод сплайнов.
Сущность этих методов заключается в доопределении поверхности в промежутках между заданным точечным каркасом с соблюдением плавного изменения кривизны. Поверхность разбивается на ячейки, которые стыкуются между собой с заданной степенью гладкости.
Далее даются элементы параметрической геометрии, теория каркаса, математическое моделирование линейчатых поверхностей, поскольку автомобильная дорога состоит из линейчатых поверхностей.
Гл. 2 содержит рассмотрение вопросов, касающихся проектирования автомобильных дорог в настоящее время.
Здесь уточняется терминология с точки зрения геометрии, указываются основные геометрические аспекты проектирования дорог, дается обобщенный алгоритм решения при системном подходе.
Гл. 3 – геометрическое и математическое моделирование линейных и поверхностных форм автомобильных дорог.
В этой гл. предлагается моделирование оси автомобильной дороги с помощью сплайна

 Отсюда модель оси, заданной системой базовых точек, представляется в виде:
Отсюда модель оси, заданной системой базовых точек, представляется в виде:
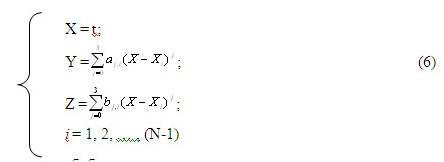
Затем представлены обобщенные геометрическая и математическая модели поверхностных форм автомобильных дорог, которые из задания четырехпараметрического множества прямых:
 |

превращаются в систему:

Далее разрабатываются обобщенные геометрическая и математическая модели линейных форм автомобильных дорог, к которым принадлежат кромка проезжей части, бровка земляного полотна.
Предлагается модель поверхности откоса.
Предлагается получение проектных горизонталей поверхностных форм автомобильных дорог, необходимых для решения задач вертикальной планировки.
В 4 гл. даются локальные особенности автомобильных дорог на виражных участках.
Гл. 5 посвящена разработке математического обеспечения визуализации линейных и поверхностных форм автомобильных дорог (рис. 1).

Рис. 1. Перспектива участка дороги
Детали можно посмотреть в монографии «Моделирование автомобильных дорог» [13].
1. Bubennikov A. V. descriptive geometry / A. V. Bubennikov. - M.: Higher school, 1985. - 228 p.
2. Bubennikov A. V. Surfaces with directing plane: Dis. kand. tech. Sciences. - M., 1955.
3. Ivanov G. S. Designing of technical surfaces. - M.: Mashinostroenie, 1987. - 192 p.
4. Koch V. N. Education and analysis of kinematic surfaces forming a permanent // Lviv house of scientists. Section ing. graphics. - Lviv, 1959. - Vol. 1. - S. 33-50.
5. Osipov V. A. computer-aided design methods of continuous-frame surfaces. - M.: Mashinostroenie, 1979. - 248 p.
6. Ryzhov N. N. Algorithmic output equations of the ruled surfaces given preassigned conditions // Prikl. geometry and eng. graphics. - Kiev: Budulinek, 1972. - Vol. 14. - P. 3-8.
7. Ryzhov N. N. The algorithms of the transition from structurally-kinematic tasks to the analytical surface // Proceedings of PFU named. Lumumba. - M., 1971. - T. 53. - Vol. 4. - S. 17-25.
8. Ryzhov N. N. Frame theory and the task of constructing surfaces // Proceedings of PFU named. Lumumba. - M., 1967. Vol XXVI: Mathematics. - Vol. 3: Applied geometry. - P. 3-17.
9. Ryzhov N. N. The determinant of the surface and its application // Proceedings of PFU named. Lumumba. - M., 1971. Vol 53: Applied geometry. - Vol. 4. - P. 3-16.
10. Ryzhov N. N. On the theory of frame // Proceedings of PFU named. Lumumba. - M., 1963. - V. 11: descriptive geometry. - Vol. 1. - C. 9-19.
11. Ryzhov N. N. A formal system of encryption of drawing surface // interuniversity collection of: descriptive geometry and its applications. - Saratov: Saratov University, 1976. - Vol. 1. - P. 20-28.
12. Sal´kov N.. According to the kinematic rotating spaces / N.. Sal´kov // Geometry and graphics. - 2013. - Volume 1. - No. 1 - Pp. 4-10. - DOI:https://doi.org/10.12737/2074.
13. Sal´kov N. A. Modeling of roads [Electronic resource] / N. A. Sal´kov. - M.: INFRA-M, 2012. - 120 p
14. Sal´kov N. A. Parametric geometry in geometric modeling / N.. Sal´kov // Geometry and graphics. - 2014. - T. 2. - No. 3. - P. 7-13. -DOI:https://doi.org/10.12737/6519.






