Energia IT Ltd. (Department of Development, Head of Development Department)
University of Technology
Korolev, Moscow, Russian Federation
Moscow, Russian Federation
The paper considers the problem of effective management of the parameters of the advertising strategy of a moving company, as an important element in promoting a new service. Based on models of the system dynamics of J. Forrester and introduction of F. Bass innovations implemented in the simulation environment AnyLogic, the dependence of the advertising campaign budget on the parameters of the advertising strategy was investigated. Optimization experiments on the simulation model allowed using the methods of experiment planning to construct a polynomial regression model approximating the simulation model. The practical application of the regression model instead of the simulation model simplifies the process of managing the parameters of the advertising strategy of the moving company.
moving; innovations; advertising strategy; budget; system dynamics; model; optimization.
Введение
Острая конкуренция на рынках товаров и услуг заставляет предприятия очень часто модернизировать свою продукцию, предлагать новые образцы, существенно или радикально отличающиеся от существующих собственных или продуктов конкурентов. Новая продукция часто связана с большим риском остаться невостребованной рынком. Поэтому любой поставщик вынужден строить оптимальную компромиссную стратегию, балансирующую между двумя крайностями:
- минимально модернизировать свой продукт. Тогда он останется узнаваемым на рынке и не потребует дополнительных усилий по его продвижению. Однако, его новой функциональности может быть недостаточно для обеспечения необходимого уровня конкурентоспособности;
- создать инновационный продукт, новый на рынке, а значит и еще не известный потенциальным покупателям. В этом случае потребуются дополнительные затраты времени и средств на его продвижение.
Задача выбора между этими вариантами является непростой т.к. содержит много параметров, связанных между собой неочевидными зависимостями, а сам процесс вывода нового продукта на рынок реализуется в нестационарной динамической среде. Одним из важных инструментов поддержки принятия подобных решений, позволяющих строить правдоподобные оценки вариантов, являются экономико-математические модели [1-5] и средства имитационного моделирования [6]. Можно выделить два основных аспекта использования этого инструментария:
- Анализ существующего объекта (или процесса). На основании существующих данных о системе и имеющейся статистики продаж построить адекватную модель, откалиброванную по этим данным, а затем на модели провести необходимые исследования, оценить варианты модернизации, развития и выбрать оптимальный вариант стратегии поведения предприятия. Такой подход применим в случае не радикального изменения поведения предприятия.
- Синтез нового объекта (или процесса). Построение предприятия «с нуля» или радикальная перестройка деятельности компании, выход на новый рынок и т.п. В этом случае в задаче выбора содержится гораздо больше неизвестных и неопределенности. Выведение на рынок инновационного продукта относится к этой группе задач.
Прикладной областью в данной работе является сравнительно новый для нашей страны вид логистических услуг – мувинг (мувинговые услуги) [7, 8]. Он, как правило, включает такой спектр услуг как переезд «под ключ», услуги упаковки, доставки и т.п. Как показано в ряде работ, в том числе в работах авторов [7, 8], адекватным инструментарием для указанного типа задач могут служить модели внедрения инновационных продуктов Ф. Басса [9] и средства имитационного моделирования, в частности, программного комплекса многоподходного моделирования AnyLogic [6]. В работах [7, 8] были рассмотрены задачи анализа деятельности мувинговой компании, а в данном исследовании эта компания рассматривается в плане синтеза, с учетом возможности вариации параметров и структуры в широком диапазоне.
Основная цель исследований, представленных в данной работе, состоит в определении оптимальных параметров рекламной стратегии [10, 11], в частности, уровня издержек на рекламную кампанию, для обеспечения охвата целевой доли рынка.
Имитационная модель
Инструментарием для исследования послужили экономико-математические модели и средства имитационного моделирования [1-9].
Классическая модель Ф. Басса распространения инноваций [9], построенная в среде AnyLogic на основе элементов системной динамике (далее - СД) Дж. Форрестера [6], имитирует процесс превращения потенциальных покупателей нового продукта в его владельцев. Предполагается, что изначально продукт никому не известен. Для того, чтобы его начали приобретать, он рекламируется. В результате люди покупают продукт либо под воздействием рекламы, либо узнав о нем от знакомых («сарафанное радио» - имитация поведения других). Логика классической (аналитической) модели Ф. Басса основана лишь на этих двух факторах – влияние инновационной составляющей спроса (параметр  ), определяемой воздействием рекламы на потенциальных покупателей, и имитационной (параметр
), определяемой воздействием рекламы на потенциальных покупателей, и имитационной (параметр  ), определяемой «сарафанным радио». Однако данная логика, будучи переложенной на язык системной динамики, позволяет учесть в модели и другие факторы в виде дополнительных параметров компании и внешней среды, что выполнено в данной работе.
), определяемой «сарафанным радио». Однако данная логика, будучи переложенной на язык системной динамики, позволяет учесть в модели и другие факторы в виде дополнительных параметров компании и внешней среды, что выполнено в данной работе.
В числе дополняющих модель Ф. Басса факторов в имитационной модели учтен, в частности, эффект повторных покупок. Он заключается в том, что у клиентов, воспользовавшихся услугой, через некоторое время (период устаревания или полного использования продукта) вновь появляется потребность в покупке данного продукта. Для учета этого обстоятельства в модель введен дополнительный параметр  – время жизни продукта (услуги). На рис. 1а показаны результаты имитационного эксперимента с повторными покупками продукта – вторая волна продаж появляется через время
– время жизни продукта (услуги). На рис. 1а показаны результаты имитационного эксперимента с повторными покупками продукта – вторая волна продаж появляется через время  . Это приводит и к некоторым колебаниям числа потребителей продукта (рис. 1б).
. Это приводит и к некоторым колебаниям числа потребителей продукта (рис. 1б).

а) б)
Рис. 1. Динамика процессов модели с повторными покупками и учетом сезонности спроса
Эффект повторных покупок проявляется в том, что по мере насыщения рынка численность потенциальных потребителей не уменьшается до нуля, а пополняется потребностями повторных покупок.
Еще одна важная особенность, отличающая имитационную модель от классической модели Ф. Басса, заключается в возможности учета нестационарности спроса, и в частности, его сезонный характер (см. мелкие колебания на рис. 1а), что повышает адекватность модели, а значит и эффективность решений, принимаемых на ее основе. Причем сезонность может быть учтена в виде табличной функции, построенной на основе ретроспективных статистических данных работы мувинговой компании. В эту ветвь также могут быть включены и зависимости спроса от цены продукта (в данной версии работы этот фактор не учтен).
Кроме того, в имитационной модели появляется возможность более тонко выстроить рекламную стратегию компании. В состав рекламной стратегии входит не только структура и состав используемых рекламных инструментов, но и бюджет рекламной компании. Здесь учитывается лишь общий объем бюджета рекламной кампании.
Поскольку реклама играет значимую роль лишь на начальной стадии вывода продукта на рынок, через некоторое время рекламную кампанию можно остановить т.к. дальнейшее насыщение рынка будет определяться в основном покупками, вызванными общением обладателями продукта с потенциальными его потребителями. В исследовании бюджет рекламной кампании был принят постоянным (например, 100 тыс. руб. в месяц), действующий на протяжении периода финансирования (например, 2 года).
Все учтенные в СД-модели дополнительные факторы делают ее уже достаточно адекватной реальным процессам поведения инновационного продукта на рынке. Однако модель не является самоцелью исследования, она лишь инструмент для поддержки принятия решений соответствующими полномочными лицами. Построенная модель позволяет, в частности:
- Получать оценки показателей качества моделируемой системы для конкретных значений параметров имитационной модели.
- Найти оптимальные значения параметров системы, обеспечивающих максимум (или минимум) требуемым показателям. Это оптимизационная задача.
- Построить аппроксимирующую функциональную зависимость показателей качества от параметров модели по результатам экспериментов на модели. Такая аппроксимация в дальнейшем может быть использована отдельно в целях оценивания вариантов без имитационной модели.
Далее покажем возможность третьего направления в комбинации со вторым. В качестве оптимизационной задачи рассмотрена минимизация общих затрат ( ) на рекламу до момента ее отключения (
) на рекламу до момента ее отключения ( ) при условии доведения доли (
) при условии доведения доли ( на рекламную кампанию мувинговых услуг, а параметр оптимизации – продолжительность финансирования рекламы
на рекламную кампанию мувинговых услуг, а параметр оптимизации – продолжительность финансирования рекламы  .
.
Введем необходимые обозначения и приведем формализованную постановку задачи.
Модель Ф. Басса с дискретным временем имеет следующий вид [9]:
где  -ом дискретном интервале времени;
-ом дискретном интервале времени;
 – коэффициент инновации. Он отражает эффективность рекламы, т.е. степень влияния рекламы на желание купить новый продукт потенциальными покупателями, например,
– коэффициент инновации. Он отражает эффективность рекламы, т.е. степень влияния рекламы на желание купить новый продукт потенциальными покупателями, например,
 – коэффициент имитации. Отражает степень влияния общения с владельцами нового продукта на желание купить новый продукт потенциальными покупателями, например,
– коэффициент имитации. Отражает степень влияния общения с владельцами нового продукта на желание купить новый продукт потенциальными покупателями, например,
 – потенциальная емкость рынка или максимальное количество покупателей, которые могут купить данный продукт;
– потенциальная емкость рынка или максимальное количество покупателей, которые могут купить данный продукт;
Таким образом, в (1) первое слагаемое определяет количество покупателей, из числа оставшихся
Функциональная схема СД-модели [6], построенной на базовой логике Ф. Басса и расширенной за счет учета дополнительных факторов, приведена на рис. 2.
В табл. 1 приведены параметры модели и целевые показатели мувинговой компании, свойственные основным режимам ее работы.
В числе дополнений к стандартной модели Ф. Басса в СД-модель добавлены элементы, структурирующие эффективность рекламы и спрос.
Эффективность рекламы зависит от многих факторов – как используемых рекламных инструментов [7, 8], так и от бюджета рекламной кампании. В СД-модели принята экспоненциальная форма зависимости эффективности рекламы от бюджета:  - расходы на рекламу,
- расходы на рекламу,  - коэффициент эффективности рекламы - при
- коэффициент эффективности рекламы - при
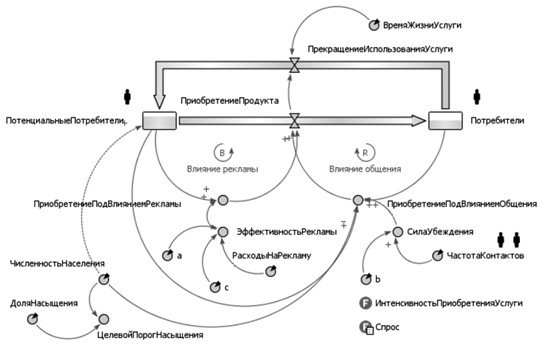
Рис. 2. Имитационная СД-модель сбыта мувинговых услуг
Таблица 1 – Основные параметры и показатели модели
|
№ |
Параметры и показатели |
Имя в модели |
Обоз- нач. |
Ед. изм. |
Значение |
|
1 |
Потенциал рынка |
Численность Населения |
|
чел. |
450000 |
|
2 |
Частота контактов владельцев продукта с потенциальными покупателями в мес. |
Частота Контактов |
f |
1/мес |
100 |
|
3 |
Время жизни продукта |
Время Жизни Услуги |
|
лет |
3 |
|
4 |
Целевой объем рынка |
Ожидаемое Насыщение |
|
чел. |
0.2 |
|
5 |
Расходы на рекламу в месяц |
Расходы На Рекламу |
|
руб. |
Варьируется |
|
6 |
Общий бюджет рекламы |
Общие расходы |
|
руб. |
Целевой показатель |
|
7 |
Время прекращения рекламной кампании |
Время Отключения |
|
лет |
Искомое |
|
8 |
Время достижения целевого объема рынка |
Время Насыщения |
|
лет |
Зависит от |
Сезонность спроса в СД-модели учтена через нормированный коэффициент сезонности спроса  – масштабный согласующий коэффициент имитационной составляющей.
– масштабный согласующий коэффициент имитационной составляющей.
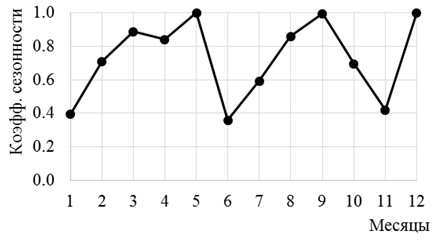
Рис. 3. Нормированный коэффициент сезонности спроса
Структурированный коэффициент инновации может быть представлен в следующем виде:  – масштабный согласующий коэффициент инновационной составляющей.
– масштабный согласующий коэффициент инновационной составляющей.
Оптимизация рекламной стратегии
Отдельный прогон имитационной модели позволяет получить значения показателей при определенном наборе значений параметров. Графики измерения некоторых показателей приведены на рис.1. Однако, реализованный в прогоне вариант рекламной стратегии в общем случае не является оптимальным.
Один из вариантов оптимальной стратегии использования рекламы заключается в том, что в определенный (оптимальный) момент времени  компания прекращает рекламировать услугу. При этом предполагается, что к некоторому, возможно другому, моменту времени
компания прекращает рекламировать услугу. При этом предполагается, что к некоторому, возможно другому, моменту времени  должно быть достигнуто желаемое количество потребителей (целевой объем рынка
должно быть достигнуто желаемое количество потребителей (целевой объем рынка  ) при минимальных общих затратах на рекламу
) при минимальных общих затратах на рекламу  . Целевой порог освоенного рынка мувинговых услуг может быть выбран, например, равным 20% от общей численности потенциальных покупателей (т.е.
. Целевой порог освоенного рынка мувинговых услуг может быть выбран, например, равным 20% от общей численности потенциальных покупателей (т.е.
при ограничениях:
где неформализованное выражение
Решить задачу (2) - (3) для фиксированных значений набора параметров модели (рис. 2, табл. 1) можно с помощью такого средства AnyLogic, как «Оптимизационный эксперимент». Для значений параметров, приведенных в табл. 1 и в тексте выше, результаты оптимизации представлены на рис. 4. В эксперименте выполнено 500 прогонов СД-модели. Параметры варьировались случайным образом в соответствии с равномерным распределением в прямоугольнике:
Рис. 4. Результаты отдельного оптимизационного эксперимента
Регрессионная модель сбыта мувинговых услуг
Использование СД-модели для управления рекламными проектами в реальной практике работы мувинговой компании является маловероятным т.к. требует квалифицированного специалиста в области моделирования. В этой связи представляется разумным построение на основе СД-модели ее многофакторной регрессионной аппроксимации, которая в дальнейшем может быть использована, например, в среде MS Excel. В качестве факторов выбраны те параметры (см. рис. 4), которые могут претерпевать изменения в процессе реализации рекламных проектов в ходе управления продвижением мувинговых услуг.
Из девяти параметров СД-модели выбраны в качестве факторов лишь пять т.к. остальные остаются неизменными или уже участвуют в Оптимизационном эксперименте (рис. 4). В табл. 2 приведены эти факторы-параметры и диапазоны их варьирования при выполнении прогонов (Оптимизационных экспериментов на СД-модели) и сборе статистики, необходимой для построения многофакторного уравнения регрессии.
Таблица 2 – Параметры регрессионной модели
|
№ |
Параметры и показатели |
Фак-тор |
Ед. изм. |
Интервал варьирования |
|
|
от |
до |
||||
|
1 |
Численность населения |
|
чел. |
100000 |
450000 |
|
2 |
Частота контактов |
|
1/мес |
100 |
1000 |
|
3 |
Время жизни услуги |
|
лет |
3 |
5 |
|
4 |
Доля рынка |
|
- |
0.1 |
0.2 |
|
5 |
Коэфф. эффективности рекламы |
|
руб. |
0.0001 |
0.000001 |
Каждый прогон на СД-модели требует определенного времени, а полученное значение целевого показателя (см. рис. 4), обладающему некоторым рассеиванием - повторные эксперименты не обладают абсолютной воспроизводимостью, т.е. при одинаковых значениях параметров решения в прогонах различаются. Это приводит к необходимости проведения серий повторных экспериментов в каждой точке факторного пространства с последующим осреднением. В целях минимизации количества прогонов, необходимых для построения регрессионной модели, следует воспользуемся инструментарием оптимального планирования экспериментов [12]. В результате оптимального экспериментирования на СД-модели и последующей обработки, была построена регрессионная модель следующего вида:
Существенные отличия в значениях коэффициентов в (4) объясняются тем. что факторы, входящие в модель, используются в своей исходной размерности, а не в нормированной форме. Модель (4) адекватна в области варьирования факторов, приведенной в табл.4, в другой области параметры модели могут быть иными. В практике управления эту область следует выбирать как можно уже, исходя из потребности в возможной вариации значений факторов.
Если логика и структура СД-модели остается адекватной моделируемому процессу сбыта продукции мувинговой компании, то построенная ее регрессионная аппроксимация может быть использована отдельно, например, в составе корпоративной информационной системы предприятия для обеспечения рекламной поддержки продвижения продукции. При внесении изменений в логику сбыта могут быть внесены коррективы и в СД-модель и ее регрессионную аппроксимацию можно построить заново.
Выводы
1. Реализованная в среде AnyLogic модель продвижения мувинговых услуг, как инновационного продукта основана на технологии системной динамики Дж. Форрестера, логике Ф. Басса и реальной статистике экономической деятельности компании. Модель, в отличие от существующих, содержит ряд дополнительных параметров и частных моделей, что повышает степень адекватности, а значит позволяет на основе ее результатов строить более эффективные стратегии продвижения продукта.
2. Построенная имитационная модель позволяет выбирать оптимальное время завершения рекламной кампании, обеспечивающее минимизацию объема рекламного бюджета мувинговой компании при условии охвата продажами целевой доли рынка и при фиксированных значениях остальных параметров СД-модели.
3. На основе имитационной СД-модели построена и более универсальная аналитическая модель, представленная уравнением множественной регрессии, увязывающим оптимальные расходы со всеми основными параметрами модели. Такая аналитическая аппроксимация построенной оптимизационной имитационной СД-модели позволяет не использовать имитацию при изменении таких параметров как число контактов, время жизни услуги и других. Многофакторная регрессионная модель, являясь адекватным отражением детальной имитационной модели процесса рекламной поддержки сбыта, позволяет существенно упростить систему управления продвижения мувинговых услуг в регионе.
1. Vilisov, V.Ya. Adaptivnyy vybor upravlencheskih resheniy. Modeli issledovaniya operaciy kak sredstvo hraneniya znaniy LPR [Tekst] / V.Ya. Vilisov. - Saarbryuken (Germaniya): LAP LAMBERT Academic Publishing. - 2011. - 376 s.
2. Vilisov, V.Ya. Metody vybora ekonomicheskih resheniy. Adaptivnye modeli [Tekst] / V.Ya. Vilisov. - M.: Finansy i statistika. - 2006. - 228 s.
3. Vilisov, V.Ya. Instrumenty vnutrennego kontrolya [Tekst] / V.Ya. Vilisov, I.E. Sukov. - M.: RIOR, INFRA-M. - 2016. - 262 s. - DOI:https://doi.org/10.12737/11472.
4. Vilisov, V.Ya. Infrastruktura innovaciy i malye predpriyatiya: sostoyanie, ocenki, modelirovanie [Tekst] / V.Ya. Vilisov, A.V. Vilisova. - M.: IC RIOR, NIC INFRA-M. - 2015. -228 s. - DOI:https://doi.org/10.12737/4320.
5. Taha, H.A. Vvedenie v issledovanie operaciy [Tekst]: Per. s angl. / H.A. Taha. - M.: Izd. dom Vil'yams. - 2005. - 912 s.
6. Oficial'nyy sayt AnyLogic [Elektronnyy resurs]. - URL: http://www.anylogic.com/ . - Data obrascheniya: 28.04.2017.




















