This paper presents an analysis of sheets of surfaces by quasi-rotation in order to prove the possible union of sheets of these surfaces. The surfaces for the study are constructed using computer mathematical modeling. The algorithm that is used to construct planes is based on a mathematical description of the method of rotating a point around a second-order axis curve. To prove the unification of some sheets of the same surface, requirements were put forward based on mathematical analysis. The results of the study allowed us to analytically prove the union of sheets.
rotation, quasi-rotation, shaping, curve axis, circle, ellipse, Dupin's cyclide, cyclic surfaces, axis of rotation, high-order surface, high-order curve
В ранее изданных статьях [1−5] описываются методы квазивращения. В статье [1] приведено конструктивное описание метода в виде графических построений, а в статьях [2, 3, 4, 5] изложено его математическое описание. Метод позволил моделировать поверхности путём вращения образующей линии вокруг осей второго порядка. На основе математического описания построений был создан алгоритм в программе «Maple», который позволил создавать модели поверхностей квазивращения.
В другой статье, связанной с квазивращением [6], упоминается уменьшение количества листов поверхностей квазивращения, которое авторы не могут объяснить аналитически, при прохождении образующей через фокус кривой оси второго порядка.
Подобные случаи без отображения циклид Дюпен показаны на рис. 1. На нём разными тонами показаны проекции листов, а также взаимное расположение образующей и оси вращения. Визуально листы объединяются в один. На каждой поверхности отдельными тонами выделены пары переходных окружностей, одна из которых обозначена буквой k.
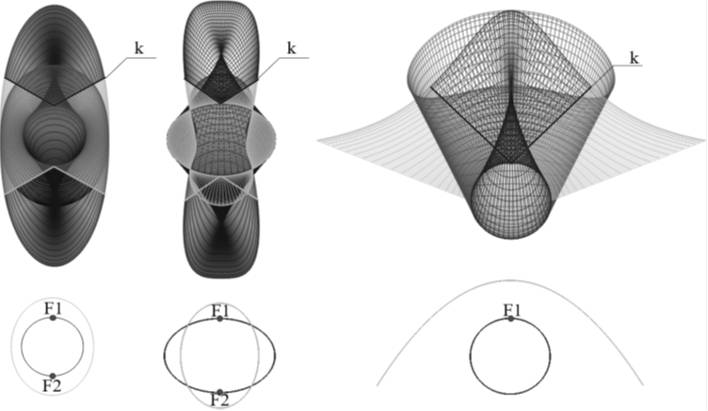
Рис. 1. Поверхности квазивращения, образующие которых
проходят через фокусы осей
В данной работе рассматриваются изменения геометрии листов исследуемых поверхностей при приближении образующей к точке фокуса. На рис. 2 показаны 2 листа, для которых центр образующей окружности совпадает с центром эллиптической оси, а её радиус стремится или равен фокусному расстоянию оси. В силу технического ограничения математической среды в графическом редакторе были добавлены более точные детали некоторых листов. На рис. видно, как часть первого листа в момент возможного объединения вырождается и переходит в циклиду Дюпена (3 на рис. 2, в), а потом из циклиды Дюпена становится частью второго листа.

Рис. 2. Проекции двух листов поверхности при приближении радиуса образующей
окружности к значению фокусного расстояния эллиптической оси:
а, б) R<c, в) R=c, г, д) R>c.
Для доказательства объединений двух листов необходимо доказать, что у них совпадают:
• предельные радиусы окружности квазивращения;
• предельные углы наклона плоскостей, в которых лежат окружности квазивращения;
• частные производные в точках предельных окружностей квазивращения (градиенты).
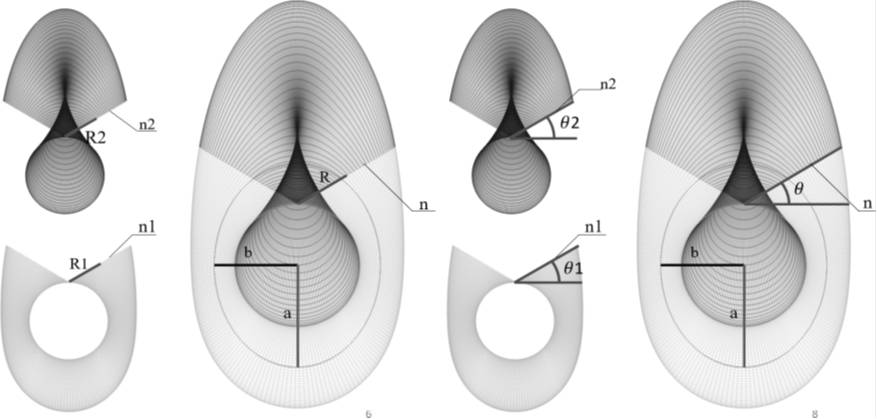
Рис. 3. Радиусы окружностей и углы наклона плоскостей

Рис. 4. Частные производные
С помощью формул, использованных в математической среде, для построения листов были получены их частные варианты для точки образующей, проходящей через фокус оси для образующей окружности и осью-эллипсом, у которых совпадают центры. Данные формулы оказались равны, из чего следует, что R1=R2=R и θ1=θ2=θ (рис. 3). На рис. 4 изображены графики частных производных для точек на получившихся окружностях и наложение этих графиков друг на друга.
Таким образом, получается, что листы одного фокуса действительно объединяются в один, если точка образующей проходит через этот фокус, а выродившийся лист заменяется циклидой Дюпена. Также стоит отметить, что окружности, к которым стремятся листы, не принадлежат ни одному из них, а являются образующими окружностями циклиды Дюпена. Таким образом, математически верным будет рассматривать листы поверхности квазивращения как единый геометрический объект.
1. Beglov I.A. Metod vrascheniya geometricheskih ob'ektov vokrug krivolineynoy osi / I.A. Beglov, V.V. Rustamyan // Geometriya i grafika. - 2017. - T. 5. - №3. -S. 45-50. -DOI:https://doi.org/10.12737/article_59bfa4eb-0bf488.99866490.
2. Beglov I.A. Matematicheskoe opisanie metoda vrascheniya tochki vokrug krivolineynoy osi vtorogo poryadka / I.A. Beglov, V.V. Rustamyan, I.V. Antonova // Geometriya i grafika. - 2018. - T. 6. - №4. -S. 39-46. - DOI:https://doi.org/10.12737/article_5c21f6e832b4d2.25216268.
3. Antonova I.V. Matematicheskoe opisanie vrascheniya tochki vokrug ellipticheskoy osi v nekotoryh chastnyh sluchayah/I.V Antonova, I.A. Beglov, E.V. Solomonova // Geometriya i grafika. - 2019. - T. 7. - №3. - S. 36-50. -DOI:https://doi.org/10.12737/article_5dce66dd9fb966.59423840.
4. Beglov I.A. N-n-digitinterrelations between the setswithin the R 2 plane generated by quasi-rotation of R 3 space // Journal of Physics: Conference Series. - 2020. - Vol. 1546 -DOIhttps://doi.org/10.1088/1742-6596/1546/1/012033.
5. Beglov I.A. Computer geometric modeling of quasi-rotation surfaces // Journal of Physics: Conference Series. - Vol 1901. - DOI:https://doi.org/10.1088/1742-6596/1901/1/012057
6. Dvoreckov P.A. Opredelenie poryadka poverhnostey kvazivrascheniya graficheskim sposobom / Dvoreckov P.A., Getmanskaya V.K. // Zhurnal tehnicheskih issledovaniy. - 2020 - T. 6, № 3 - S. 27-34.
7. Antonova I.V., Solomonova E.V., Kadykova N.S. Matematicheskoe opisanie chastnogo sluchaya kvazivrascheniya fokusa ellipsa vokrug ellipticheskoy osi // Geometriya i grafika. - 2021. -T. 9. - №1. - S. 39-45. - DOI:https://doi.org/10.12737/2308-4898-2021-9-1-39-45






