in interactive control and management systems for difficult dynamic objects it is necessary to provide a possibility of adequate perception by the person of the provided information for acceptance of conscious and effective managing actions. In work the new class of representations promoting the solution of the designated problem is offered.
pulse a signal, an archetype, amplitude-time characteristics, the modeling function
Использование пульсовых сигналов лучевой артерии в задачах медицинской диагностики предполагает формализацию пульсовых сигналов, в том числе, путем создания их моделей. Для практической реализации имитационного моделирования сигналов определим их как два архетипа, в смысле исходных базовых образцов, отличия от которых в конкретных пульсовых сигналах вызываются физиологическими особенностями организма. При этом проявляется свойство полиаттракции [1] – одна часть сигналов лучше коррелирует с первым архетипом, а другая часть, соответственно со вторым. Первый архетип назовем S-архетипом (archetype S) – от англ. susceptible (восприимчивый), а второй - V–архетипом (archetype V) - от англ. viscous (вязкий).
На рис. 1 показаны сигналы, характерные для каждого из архетипов. Здесь и далее A – амплитуда сигнала, t – время. Формально перевод формы из одного архетипа в другой можно осуществить применением к S-архетипу операции интегрирования, а к V-архетипу – операции дифференцирования, что иллюстрирует штриховая линия на рис. 1б.
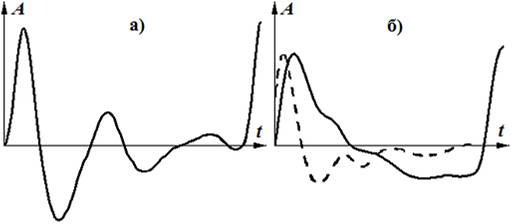
Рис. 1. S-архетип (а) и V-архетип (б) пульсовых сигналов
Далее рассматриваются случаи S-архетипа. Визуально форма одного периода сигнала S-архетипа выглядит как типичное затухающее вынужденное колебание, вызванное импульсным воздействием (в данном случае порцией крови, поступившей в лучевую артерию в область запястья), что использовалось и ранее для моделирования пульсового сигнала [2]. При этом на форму зарегистрированного сигнала влияют различные факторы: особенности датчика пульса, физические нагрузки, эмоциональное состояние, физиологические особенности организма, в том числе эластичность кровеносных сосудов, зависящая в большей степени от возраста и т.д. [3].
Также форма сигнала может иметь в различной степени выраженные особенности, связанные с локальными процессами, протекающими в лучевой артерии в области съема сигнала [4]. На рис. 2 представлен один период сигнала S-архетипа с достаточно выраженным проявлением эффекта искажения формы затухающего колебательного процесса.

Рис. 2. Иллюстрация «симптоматических» дуг д1, д2 и д3
Возможно это проявление эффекта отражения волны от ареала бифуркаций. Под ареалом бифуркаций понимается иерархия разветвлений лучевой артерии, последовательно и древовидно располагающихся за точкой съема пульса, причем, наиболее заметный эффект порождает первое ответвление. Для подчеркивания проявленных локальных особенностей на рис. изображены «симптоматические дуги» дуги д1, д2 и д3, аппроксимирующие и подчеркивающие эти локальные особенности, AS – амплитуда «систолического» зубца, tS – время его появления, AF – амплитуда «дикротического» зубца, tF – время его появления.
Введем понятие универсальной моделирующей аутигенной функции (УМАФ) fu(t), имеющей двойственный характер – с одной стороны функциональная зависимость может отобразить влияние различных факторов, с другой – она аутигенна, т.е. ее применение справедливо для моделирования в определенном локализованном интервале времени:
fu(t) = au(t-τu) h(t-τu) Sin(2π mu du(t-τu)+φu) (1+h(t-τb) (bu(t-τb)–1))+cu,
где: au – амплитудная модуляционная функция, реализующая эффект затухания вынужденного колебания, вызванного импульсным воздействием; h – функция Хевисайда; bu – мультипликативная составляющая для дополнительного микширования (подавления) сигнала – отражает эффект суммарного противодействия различных внутрисистемных факторов проявлению внешнего воздействия, реализуемого после уменьшения амплитуды вынужденного колебания до некоторого сопоставимого (с потенциальным уровнем силы противодействия) уровня в процессе его затухания (гипотетическое проявление «локального» гомеостаза); cu – аддитивная составляющая, вызванная ненулевым средним значением сигнала; du – функция дисторсии времени, отражающая нарушение периодичности колебательного процесса из-за нелинейности системы; mu – масштабирующая временная константа, определяющая начальную частоту моделирующего колебания; φu – начальная фаза моделирующего колебания; τu – начальная временная точка действия УМАФ; τb – начальная временная точка действия bu.
В приведенной формуле:
au(t≤(τu+Δ)) = au(τu); au(t>(τu+Δ)) = au(τu)*e-γσ; σ = (t-τu-Δ)2;
γ – степень нелинейности; Δ – интервал инерции, отодвигающий начало заметного влияния силы, вызывающей затухание амплитуды колебаний; h(t<0) = 0, h(t≥0) = 1; cu(t) = tρ; ρ – степень нелинейности.
Запишем выражение для имитационной моделирующей функции fp(t), моделирующей один период сигнала, начиная с момента tS (рис. 2):
fp(t) = fg(t) + fr(t) + fw(t),
где: fg(t) – основная функция, моделирующая затухающее вынужденное колебание, вызванное импульсным воздействием; fr(t) – корректирующая функция, моделирующая предположительно отраженную от ареала бифуркаций волну вынужденного колебания (см. выше); fw(t) – вспомогательная технологическая функция, моделирующая «рябь» или иные процессы, иногда проявляющиеся в наблюдаемой зоне.
Все функции являются УМАФ. Составляющая fr(t) может отсутствовать. Еще реже возникает необходимость использования компоненты fw(t). Параметры функций определяются по экспериментальным данным [5]. Так, начальная частота основной функции лежит в диапазоне 3,5…5 Гц, а частота корректирующей функции более чем 6-7 Гц. Различие частот затухающего колебания и отраженной волны можно объяснить нелинейностью системы и особым характером формирования отраженной волны. Развернутое выражение пульсовой имитационной моделирующей функции:
fp(t) = ag(t-τg)hg(t-τg)Sin(2πmgdg(t-τg)+φg)+ar(t-τr)hr(t-τr)Sin(2πmrdr(t-τr)+φr)+
aw(t-τw)hw(t-τw)Sin(2πmwdw(t-τw)+φw).
где: φg = π/2, φr = 0, φb = 0; τg – момент систолического максимума выбранного периода сигнала (ts на рис. 2); ag(t=τg) = As, интервал инерции для этой составляющей не более Ω4 (четверть длительности первого периода вынужденного колебания); ar(t=τr) = (0,1…0,2) As, интервал инерции менее Ω4.
Для упрощения убраны мультипликативные и аддитивные составляющие. Величина масштабной временной константы mg определяется, исходя из начальной частоты моделирующего колебания в диапазоне 3,5…5 Гц. Масштабная константа mr определяется, исходя из начальной гипотетической частоты отраженной волны, величиной более чем 6-7 Гц. При этом расстояние от τg до τr чуть более Ω4. Отметим существенное различие частот затухающего колебания и отраженной волны, что объясняется не только нелинейностью системы, но и особым характером формирования отраженной волны.
Заметим, что, в отличие от теоретического импульсного воздействия, импульс порции крови, поступающей в область съема пульса, растянут по времени, а также что наблюдаемый процесс не является затухающим колебанием в классическом виде, а лишь имитируется как таковой.
1. Guchuk V.V. Technology objectification peer clustering weakly formalized objects / Bulletin USATU, 2014. V. 18. I. 5. Pp. 149-154.
2. Wouter Huberts, Koen Van Canneyt UGent, Patrick Segers UGent. Experimental validation of a pulse wave propagation model for predicting hemodynamics after vascular access surgery. // Journal of Biomechanics, 2012, I. 45 (9), pp. 1684-1691.
3. Ilyukhin OV, Lopatin YM pulse wave velocity and elastic properties of the main arteries VolGMU // Bulletin, 2006, I. 1, pp. 3-8.
4. Boronoev V.V. Analysis of pulse wave in an automated mode // Biomedical Engineering, 2014, I. 4, pp. 33-36.
5. Guchuk VV Applied formalization of the local simulation of the pulse signal of radial artery // Inter-Medical, 2015, I 2, pp.12-17.






