г. Москва и Московская область, Россия
Москва, г. Москва и Московская область, Россия
ГРНТИ 67.11 Строительные конструкции
ГРНТИ 67.01 Общие вопросы строительства
ОКСО 08.02.02 Строительство и эксплуатация инженерных сооружений
ББК 222 Механика
ББК 30 Техника и технические науки в целом
ББК 38 Строительство
ББК 385 Строительные конструкции
ББК 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
ТБК 50 Технические науки в целом
ТБК 5014 Техническая физика
ТБК 54 Строительство
ТБК 5414 Строительные конструкции
Ферма с одной неподвижной шарнирной и тремя подвижными опорами имеет двойную крестообразную решетчатую структуру. Выводятся аналитические зависимости прогиба от числа панелей. Уравнения для определения усилий в стержнях решаются в символьной форме в системе компьютерной математики Maple. Применяется формула Максвелла - Мора и метод индукции для получения общего решения.
Ферма, прогиб, формула Максвелла- Мора, Maple
Расчет перемещений узлов фермы, необходимый для оценки ее деформативности, обычно выполняют численно в одном из стандартных пакетов. С увеличением числа стержней в ферме увеличивается и размер матрицы уравнений равновесия узлов. Начиная с некоторого значения, любой численный метод начинает давать погрешности, недопустимые, если речь идет о таких ответственных расчетах, как расчеты мостов, покрытий промышленных сооружений, концертных залов, стадионов. Именно в таких сооружениях как правило применяются фермы с большим числом панелей. В работах [1-3] показано, что для многих статически определимых стержневых регулярных (с периодической решеткой) ферм возможно получить формульное решение, свободное от упомянутого "проклятия размерности". Аналитические решения для пространственных [4-10] и плоских ферм [11-19] получены с использованием системы компьютерной математики Maple и метода индукции. В настоящей работе на основе программы [20] для нахождения усилий в стержнях статически определимых фермах и упомянутого метода индукции выводятся формулы для прогиба центрального узла плоской фермы (рис. 1). Ферма с n панелями (считаются по нижнему поясу) содержит m=4n+18 стержней и 2n+9 сочленяющих узлов. Ферма статически определима, однако из трех уравнений равновесия конструкции в целом (как это обычно делается в начале расчета) найти пять реакций не удается. Это связано с тем, что ферма без опор не является жестким телом и имеет две степени свободы. Отсюда неизбежно применения полного расчета фермы вырезанием всех узлов и составление общей системы равновесия.
1. Рассмотрим решение задачи о действии сосредоточенной силы. В программу [20] вводятся координаты узлов, порядок соединения стержней и узлов. Результатом расчетов являются аналитические выражения для усилий. Смещение вычисляется по формуле Максвелла – Мора
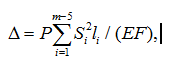
где — усилия в стержнях фермы от действия единичной нагрузки P,
— длины стержней, EF — жесткость стержней (принята одинаковой для всех стержней). Принимается четное число панелей n=2k. Суммирование ведется по всем стержням, кроме опорных. В процессе счета было замечено, что при k=2,5,8... определитель системы уравнений равновесия обращается в ноль. Для того, чтобы исключить эти значения из метода индукции для параметра k выбирается закон изменения
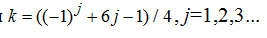

Рис.1. Ферма при значениях
Получено следующее выражение для прогиба
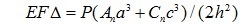 (1)
(1)
где  . Методом индукции найдены коэффициенты
. Методом индукции найдены коэффициенты
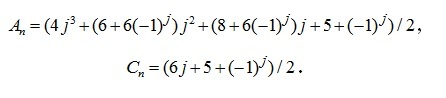
Для этого из решений для ферм с числом панелей от 1 до 14 были выявлены последовательности коэффициентов перед кубами линейных размеров a и c соответственно:

Оператор rgf_findrecur из пакета genfunc системы Maple по этим данным дал рекуррентные уравнения, которым удовлетворяют члены последовательностей:
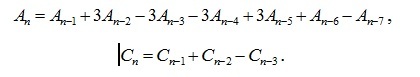
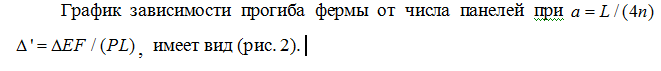
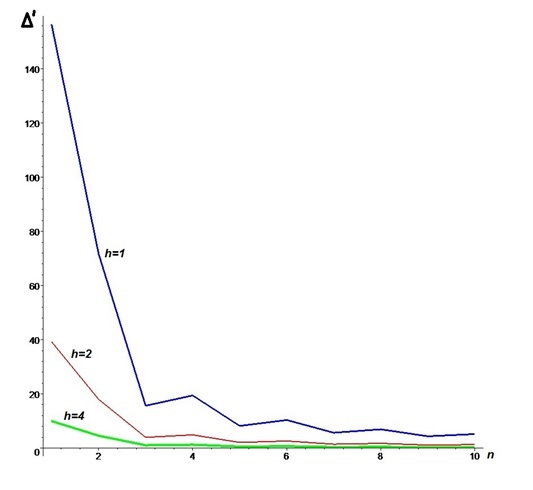
Рис.2. График зависимости прогиба фермы от числа панелей, L=100м
Одновременно с выводом формулы для прогиба можно получить и формулы для расчета реакции опоры стержней. Горизонтальная компонента реакции неподвижной опоры: . Вертикальные реакции подвижных опор:
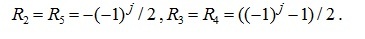
2. Рассчитаем в (1) коэффициенты от распределенной нагрузки ( рис.3).
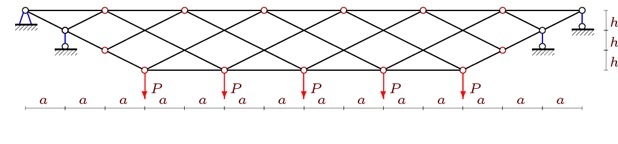
Рис.3. Ферма с распределенной нагрузкой
Методом индукции получено
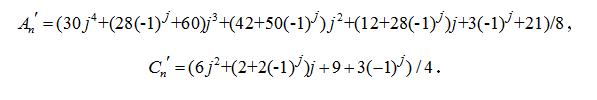
Для этого из решений для ферм с числом панелей от 1 до 18 были выявлены последовательности коэффициентов перед кубами линейных размеров a и c соответственно:
7, 207, 399, 1871, 2811, 7683, 10315, 21771, 27423, 49703, 60087, 98487, 115699, 176571, 203091, 293843, 332535, 461631
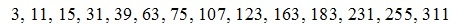
Оператор rgf_findrecur из пакета genfunc системы Maple по этим данным дал рекуррентные уравнения, которым удовлетворяют члены последовательностей:
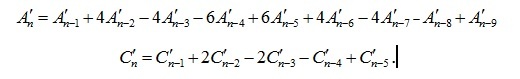 .
.
1. Hutchinson R. G., Fleck N.A. Microarchitectured cellular solids - the hunt for statically determinate periodic trusses // ZAMM Z. Angew. Math. Mech. 2005. 85, No. 9, Pp. 607-617.
2. Hutchinson R.G., Fleck N.A. The structural performance of the periodic truss // Journal of the Mechanics and Physics of Solids. 2006. Vol. 54. No. 4. Pp. 756-782.
3. Zok F. W., Latture R. M., Begley M. R. Periodic truss structures // Journal of the Mechanics and Physics of Solids. 2016. vol. 96. Pp. 184-203. https://doi.org/10.1016/j.jmps.2016.07.007
4. Kirsanov M. N. Stress State and Deformation of a Rectangular Spatial Rod Cover // Scientific Herald of the Voronezh State University of Architecture and Civil Engineering. Construction and Architecture. 2016. Vol. 31. No. 3. Pp. 71-79.
5. Kirsanov M. N. Analysis of the buckling of spatial truss with cross lattice // Magazine of Civil Engineering. 2016. No. 4. Pp. 52 - 58. DOI:https://doi.org/10.5862/MCE.64.5
6. Кирсанов М.Н. Аналитическое исследование жесткости пространственной статически определимой фермы // Вестник МГСУ. 2017. Т. 12. Вып. 2 (101). С. 165-171.
7. Кирсанов М.Н., Андреевская Т.М. Анализ влияния упругих деформаций мачты на позиционирование антенного и радиолокационного оборудования // Инженерно-строительный журнал. 2013. №5(40). С. 52-58.
8. Кирсанов М.Н. Изгиб, кручение и асимптотический анализ пространственной стержневой консоли // Инженерно-строительный журнал. 2014. № 5 (49). С. 37-43.
9. Кирсанов М.Н. Расчет пространственной стержневой системы, допускающей мгновенную изменяемость // Строительная механика и расчет сооружений. 2012. № 3. С. 48-51.
10. Voropai R. A., Kirsanov M.N. On the deformation of spatial cantilever trusses under the action of lateral loads // Science Almanac. 2016. No. 9-2(23). С.17-20. DOI:https://doi.org/10.17117/na.2016.09.02.017
11. Доманов Е. В. Аналитическая зависимость прогиба пространственной консоли треугольного профиля от числа панелей//Научный альманах. 2016. №6-2 (19). С. 214-217. DOI:https://doi.org/10.17117/na.2016.06.02.214
12. Ершов Л.А Формулы для расчета деформаций пирамидального купола // Научный альманах. 2016. № 11-2(25). С. 315-318. DOI:https://doi.org/10.17117/na.2016.11.02.315
13. Tinkov D. V., Safonov A. A. Design Optimization of Truss Bridge Structures of Composite Materials // Journal of Machinery Manufacture and Reliability. 2017. Vol. 46, No. 1, Pp. 46-52. DOI:https://doi.org/10.3103/S1052618817010149
14. Астахов С.В. Вывод формулы для прогиба внешне статически неопределимой плоской фермы под действием нагрузки в середине пролета// Строительство и архитектура. 2017. Т. 5. № 2. С. 50-54.
15. Кирсанов М.Н., Суворов А.П. Исследование деформаций плоской внешне статически неопределимой фермы // Вестник МГСУ. 2017. Т. 12. Вып. 8 (107). С. 869-875. DOI:https://doi.org/10.22227/1997-0935.2017.8.869-875
16. Кирсанов М.Н. Анализ прогиба арочной фермы // Строительная механика инженерных конструкций и сооружений. 2017. - № 5. - С. 50-55
17. Кирсанов М. Н. Анализ усилий и деформаций в корабельном шпангоуте моделируемого фермой // Вестник Государственного университета морского и речного флота имени адмирала С. О. Макарова. - 2017. - Т. 9. - № 3. - С. 560-569. DOI:https://doi.org/10.21821/2309-5180-2017-9-3-560-569
18. Kirsanov M.N., Zaborskaya N.V. Deformations of the periodic truss with diagonal lattice // Magazine of Civil Engineering. 2017. No. 3. Pp. 61-67. doi:https://doi.org/10.18720/MCE.71.7.).
19. Belyankin N.A., Boyko A. Y. Analysis of the deflection of the flat statically determinate girder // Sciense Almanac. 2017. N 2-3(28). С. 246-249. https://elibrary.ru/download/elibrary_28913792_32626016.pdf
20. Кирсанов М.Н. Maple и Maplet. Решения задач механики. СПб.: Изд-во Лань, 2012. 512 с.


















