Новочеркасский инженерно-мелиоративный институт имени А.К. Кортунова
Россия
Россия
с 01.01.2010 по 01.01.2019
Новочеркасск, Ростовская область, Россия
Одним из показателей добротности научных исследований является наличие статистической обработки результатов исследований, полученных в результате закладки пробных площадей в лесокультурном производстве, а первостепенной задачей для исследователя (инженера лесного хозяйства) является доказательство факта достоверности полученных результатов. Большие возможности статистических расчётов для исследователей открываются при помощи пакета прикладных программ Mathcad (ППП Mathcad). Цель работы - детальное описание и представление математико-статистической обработки данных инвентаризации, полученных в результате закладки пробной площади и проведённогоподеревногообмера деревьев клёна остролистного (AcerplatanoidesL.) вдоль автомобильной трассы Шахтинского шоссе,трасса 60Н-248.Методология исследования состоит в том, что с использованием ППП Mathcadна конкретных примерах пошагово представлены действия и расчёты для получения основных статистических показателей, был обработан таксационный показательдиаметра на высоте 1,3 мдеревьев клёна остролистного (AcerplatanoidesL.).Главные результаты исследования: выборочная средняя диаметра 27,1 см; изменчивость диаметра характеризуется такими показателями как среднееквадратическое отклонение 9,6 см и коэффициент вариации 35,3 %, которые говорят о значительной изменчивости изучаемого признака, оценка достоверности приводит к выводу о надёжности выборочной средней, среднего квадратического отклонения, коэффициента вариации, асимметрии на 5%-ном уровне значимости. Главные выводы исследования состоят в том, что ППП Mathcad позволяет оперировать большим числом данных, быстро и с достаточной точностью обрабатывать и сравнивать результаты измерений, полученных при подеревной инвентаризации в лесном хозяйстве.
математико-статистическая обработка, лесокультурные исследования, статистическая обработка данных, достоверность результатов исследований, пакет прикладных программ Mathcad (ППП Mathcad)
Введение. Основные области исследований в соответствии с паспортом специальности 06.03.01 «Лесные культуры, селекция, семеноводство»– это изучение плодоношения, лесоводственно-таксационная оценка чистых и смешанных искусственных насаждений(закладка пробных площадей на которых определяются основные параметры, например, высота и диаметры деревьев, освещенность под пологом насаждения, текущие приросты), применение удобрений в питомниках и на лесокультурных площадях, а также другие вопросы[3,13].
Одним из показателей добротности научных исследований является наличие статистической обработки данных (результатов исследований), полученных в результате закладки пробных площадей, а первостепенной задачей для исследователя является доказательство факта достоверности полученных результатов.Зачастую, исследователи, проводя эксперимент, видят показатели, которые на первый взгляд предвещают значимые выводы[10,19].Например, Кружилин С.Н., при проведении статистической обработки заметил, что высотадуба черешчатогов лесных культурахНижнего Дона, созданных с применением разных типов смешения,в условиях сухих дубрав разнотравно-злаковой степи является не достоверной, хотя на первый взгляд она заметно больше чем у дуба, произрастающего в сухой степи [10].
В книге «Энциклопедия археологии» (Дебора М. Пирсолл, 2008)описываются способы, позволяющие избежать неправильного толкования статистических данных, включающие в себя использование надлежащей схемы и исключение предвзятости при проведении исследований [17].
Неправильное использование статистических данных может быть, как случайным, так и преднамеренным, Д.Хафф (1954) в своей книге «Как лгать при помощи статистики» излагаетряд соображений по поводу использования и неправильного применения статистических данных.В статье «Статистические методы, используемые в журналах по высшему образованию с 2006 по 2010 года» (Р. Варн, М. Лазо, Т. Рамос, и Н. Риттер,2012)[18], анализу подлежат статьи из различных журналов,проводится обзор статистических методов, используемых в определённых областях науки, в итоге авторы приходят к выводу, чтостатистические данныедолжны быть достоверны, а не должны выглядеть идеально.
Основными авторами, доступно охарактеризовавшими методики математико-статистической обработки материалов применительно к лесохозяйственным исследованиям, являются: Митропольский А.К., 1971 [12]; Зайцев Г.Н., 1984 [5]; Доспехов Б.А. [3]; Ивонин В.М., Пеньковский Н.Д., 2003 [6], Колмогоров А.Н., 2005 («Избранные труды. В 6-ти томах. Том 2. Теория вероятностей и математическая статистика»); Барышникова Е.В., 2010 [1];Танюкевич В.В., 2004, 2011 [14]; ХуснутдиновР.Ш., 2014 («Сборник задач по теории вероятности и математической статистике. Учебное пособие»), Гмурман В.Е., 2003, 2017 [2]. Например, Доспеховым Б.А. даны основы статистической обработки результатов исследований и техника математической обработки данных наблюдений, однофакторных и многофакторных полевых и вегетационных опытов [3].Ивониным В.М. и Пеньковским Н.Д.показано вычисление основных параметров статистического ряда[6]. Гмурман В.Е. большое внимание уделил статистическим методам обработки экспериментальных данных [2].
К сожалению, авторы не дают конкретные рекомендации по программному обеспечению, способному с максимальной точностью обработать результаты лесокультурных исследований, поэтомуостаются не раскрытыми вопросы в какой программе всё-таки рассчитать и сравнить результаты, полученные при подеревной инвентаризации.Нами сделана попытка с помощью пакета прикладных программMathcad(далеепо тексту – ППП Mathcad) на конкретных примерах пошагово представить действия и расчёты для получения основных статистических показателей, применительно к лесокультурным исследованиям, в чём и состоит научная новизна представленной работы.
Материалы и методы исследования. Во многих диссертационных работах в разделе «Методика проведения исследований» встречаются записи: результаты полученных измерений подвергались математической обработке на персональном компьютере с использованием пакетов прикладных программ «Statgraphics», «Biostat», «MicrosoftExcel» [11];математико-статистическая обработка материалов производилась с помощью программ STATGRAPHICS и Excel для среды MS Windows [8];для оценки достаточности количества наблюдений и достоверности полученных результатов проводилась математическая обработка, рассчитывали: М±mм, коэффициент вариации (±С,%), точность опыта (±Р,%)[10].Такие общие характеристики на фоне детализации других специализированных методик говорят о том, что у исследователей не возникает проблем с математико-статистической обработкой материалов, что статистика выполнена «общепринятыми в математике методами». Важным моментом для исследователя является понимание полученных параметров статистических показателей, уметь пользоваться ими и анализировать их. Главными недостатками,которые представляются очевидными, при обработкеполевых исследований являются:анализ большого объёма обрабатываемой информации, который требует значительные временные затраты; также при обработке данных с помощью математических методов возрастает вероятность возникновения ошибки, на устранение которой потребуется дополнительное время. Всевышеуказанные трудности имеют место приобработке данных, полученных в результате закладки пробной площади и подеревной инвентаризации и в этой связи представляется необходимойавтоматизация процесса.Отсюда и применение специализированных программ и интернет-сайтов в которых гораздо проще провести расчёт статистики. Большие возможности статистических расчётов для исследователей открываются при помощи пакета прикладных программ Mathcad (ППП Mathcad). Mathcad – это уникальный математический пакет для работы с уравнениями, числами, текстом и графиками [9]. При этом, важно отметить, что все вычисления в ППП Mathcad производятся автоматически, т.е. изменив исходные данные, мы мгновенно получаем вычисленные показатели для введённой выборки. Формулы в ППП Mathcad, в отличие от, например, программы для работы с электронными таблицами MicrosoftExcel, выглядят также, как и в учебнике по статистической обработке, что позволяет вставлять фрагменты формул, графиков и вычислений (расчётов), созданных в ППП Mathcadв текстовый редактор MicrosoftWord.
В данной работе использованы методики: подеревной инвентаризации, пробные площади заложены с учётом ОСТ 56-69-83 «Площади пробные лесоустроительные. Методы закладки»; ГОСТ 16483.6-80 (СТ СЭВ 1141-78) [3], а также различные статистические методы (аналитических группировок, индексный и структурный анализы) [5].
Целью представленной работы является детальное описание и представление математико-статистической обработки данных, полученных в результате закладки пробной площади и подеревной инвентаризации в г. Новочеркасске, с использованием ППП Mathcad[1,9], применительно к таксационному показателю –диаметр на высоте
Для выполнения поставленной цели работы нам необходимо было выполнить следующие задачис использованием ППП Mathcad:
а) записать данные, полученные в результате полевого обследования деревьев в ППП Mathcad.
б) провести первичную обработку данных наблюдения (диаметра) и построить статистическое распределение выборки с помощью встроенных функций ППП Mathcad.
в) построить полигон и гистограмму теоретической кривой нормального распределения диаметра клёна остролистного (Acerplatanoides L.) на высоте 1,3 м. Выдвинуть гипотезу о законе распределения исследуемой случайной величины по виду гистограммы (или полигона).
г) вычислить основные статистические показатели, такие как выборочная средняя, выборочная дисперсия, среднее квадратическое отклонение, коэффициент вариации, асимметрию и эксцесс с помощью ППП Mathcad.
д) найти ошибки полученных показателей и относительную ошибку выборочной средней. Пользуясь критерием Стьюдента, определить достоверность статистических показателей для 5% - ного уровня значимости.
е) при уровне значимости α = 0,05, проверить по критерию Пирсона гипотезу о нормальном распределении генеральной совокупности.
ж) вычислить доверительные интервалы для генерального среднего, для коэффициента вариации и среднего квадратического отклонения в генеральной совокупности.
з) провести анализ результатов полученных данныхс использованием ППП Mathcadматематико-статистической обработки результатов лесокультурных исследований.
В соответствии с методикой исследования [3] полевой обмер деревьев был проведён 9 и 10 октября 2017 года. Объектом исследований являлись деревья тополя пирамидального (Populuspyramidalis L.) [16]и клёна остролистного (AcerplatanoidesL.) [16], произрастающие по обеим сторонам Шахтинского шоссе, трасса 60Н-248. Исследуемая территория ограничена северным выездом из г. Новочеркасска и южным въездом п. ПерсиановскийОктябрьского района Ростовской области, протяжённость участка составляет
Рядовая посадка тополя, с примесью деревьев клёна располагается в западной части от автомагистрали, а посадка клёна на противоположной стороне от автомагистрали, в восточной части (рисунок 1).
На рисунке 2 показаны тополь пирамидальный и клён остролистный на объекте исследований, произрастающие деревья выполняют функцию придорожных насаждений. Насаждения, которые формируют придорожную полосу имеют возраст 60-65 лет.
На пробной площади при подеревной инвентаризации были проведены измерения высоты деревьев (h, м), диаметра на высоте
Все этапы математико-статистической обработки результатов, полученных при инвентаризации, расчёт основных статистических показателей и их оценка проведены с использованием ППП Mathcad [1,3], применительно к таксационному показателю (диаметр на высоте
Необходимые для расчётов в ППП Mathcad данные отражены в таблице 1.
Результаты исследования и их обсуждение. Анализируя таблицу 1, выборочная совокупность является большой выборкой, так как содержит результаты 100 наблюдений (измерений), среди значений также встречаются повторяющиеся варианты. Полученные экспериментальные данные необходимо обработать интервальным методом.

|
С |
Рис. 1. Ситуационная схема месторасположения объекта исследований [6]


А) тополь пирамидальный Б) клён остролистный
Рис. 2. Исследуемые рядовые посадки насаждений вдоль Шахтинского шоссе
Таблица 1
Данные измерения диаметра клёна остролистного (AcerplatanoidesL.)на высоте 1,3 м (d1,3, см)
|
51,8 22,8 39,5 36,9 41,2 39,2 28,0 21,3 21,3 43,6 |
39,0 22,3 29,6 19,4 25,8 26,4 35,7 34,1 32,5 23,6 |
30,4 34,4 39,5 45,5 37,3 47,8 29,6 24,2 28,7 23,9 |
43,9 16,2 32,8 32,5 43,6 23,2 35,7 41,7 32,5 16,9 |
27,1 43,0 30,9 32,5 22,0 33,8 34,2 22,3 27,1 27,4 |
22,9 19,1 43,0 15,9 14,6 13,7 24,5 30,3 34,7 22,3 |
23,9 22,6 17,8 17,8 21,0 42,4 44,9 32,5 20,4 23,2 |
26,8 21,7 22,0 20,4 22,0 22,3 15,3 17,2 32,5 22,5 |
17,2 26,1 13,1 8,9 15,6 31,1 12,1 36,3 21,0 15,0 |
11,1 16,6 20,4 22,6 21,0 10,2 22,9 26,4 18,8 13,1 |
а) Все данные по диаметру надо разбить на k интервалов одинаковой длины, это необходимо для выполнения сводки данных наблюдения за измерением деревьев по диаметру. По приближенной формуле Стерджесса определяемчисло интервалов:
(1)
где - объём выборки. Число интервалов округляем до целого числа.
Длина интервала:
(2)
где - наибольший элемент выборки;
- наименьший элемент выборки.
Вычислим длину интервала:
(см).
(см)
Границы интервалов можно рассчитатьпо следующей формуле:
(3)
б) Сводку данных наблюдений выполняем с помощью ППП Mathcad.Интервальный ряд распределения частот, полученный по сводке данных наблюдения, представлен в виде таблицы 2.Ряд распределения (статистический рядраспределения частот) содержащий значения вариант, представляющих собой величины середин каждого интервала и соответствующих им частот представлен втаблице 3 и в таблице 4 – ряд распределения относительных частот.
в) Для построения гистограммы относительных частот необходимо знать длины интервалов (основания прямоугольников) и высоты
(плотность относительной частоты), ряд распределения плотности относительной частотыпредставлен в таблице 5.На рисунке 3 представлена гистограмма относительных частот.
Таблица 2
Интервальный ряд распределения частот
|
Интервалы |
8,9–14,3 |
14,3–19,7 |
19,7–25,1 |
25,1–30,5 |
30,5–35,9 |
35,9–41,3 |
41,3–46,7 |
46,7–52,1 |
|
Частота |
7 |
15 |
29 |
14 |
16 |
8 |
9 |
2 |
Таблица 3
Статистический ряд распределения частот
|
Значение |
11.6 |
17 |
22.4 |
27.8 |
33.2 |
38.6 |
44 |
49.4 |
|
Частота |
7 |
15 |
29 |
14 |
16 |
8 |
9 |
2 |
Таблица 4
Ряд распределения относительных частот
|
Значение |
11.6 |
17 |
22.4 |
27.8 |
33.2 |
38.6 |
44 |
49.4 |
|
Относительная частота
|
0.07 |
0.15 |
0.29 |
0.14 |
0.16 |
0.08 |
0.09 |
0.02 |
Таблица 5
Ряд распределения плотности относительной частоты
|
Значение |
11.6 |
17 |
22.4 |
27.8 |
33.2 |
38.6 |
44 |
49.4 |
|
Плотность |
0.013 |
0.028 |
0.054 |
0.026 |
0.03 |
0.015 |
0.017 |
0.0037 |
Рис. 3. Полигон и гистограмма относительных частот. Теоретическая кривая нормального распределениядиаметровклёна остролистного (AcerplatanoidesL.) на высоте 1,3 м
Соединяя середины верхних сторон прямоугольников отрезками прямых линий, получаем полигон относительных частот (ломаная линия). По виду гистограммы (полигона) рисунка 3выдвигаем гипотезу о нормальном распределении признака Х – измерение диаметров клёна остролистного (AcerplatanoidesL.)на высоте 1,3 м (d1,3, см).
г) Основные статистические показатели вычислим с помощью ППП Mathcad.
Так как следовательно, изменчивость данного признака (диаметра клёна)является значительной.Так как А>0, то асимметрия – левосторонняя, потому что вершина полигона сдвинута влево относительно вершины кривой нормального распределения (пунктирная линия на рисунке 3). Эксцесс Е<0, это говорит о том, чтолиния распределения вариант данного ряда проходит ниже кривой нормального распределения.
д)Далее вычислим ошибки среднего выборочного значения, среднего квадратичного отклонения, коэффициентов вариации (%), асимметрии и эксцесса:
Путём вычисления отношения величины рассматриваемого показателя к его ошибке рассчитывается оценка достоверности показателей:
Полученные показатели достоверности сравниваем со стандартной величиной критерия Стьюдента t(k, ), при числе степеней свободы k=n–1=100–1=99(n =100) и уровне значимости
.Значения показателей достоверности для выборочной средней, среднего квадратичного отклонения, коэффициента вариации и асимметрии больше, чем
, то перечисленные статистические показатели достоверны на 5%-ном уровне значимости. Значение показателя достоверности для эксцесса меньше, чем
, следовательно, эксцесс недостоверны на 5%-ном уровне значимости, что видно и на рисунке, 3.
е)По критерию Пирсона (при заданном уровне значимости ) проверим гипотезу о нормальном распределении генеральной совокупности. Для этого необходимо найти теоретические частоты
с помощью формулы плотности нормального распределения:
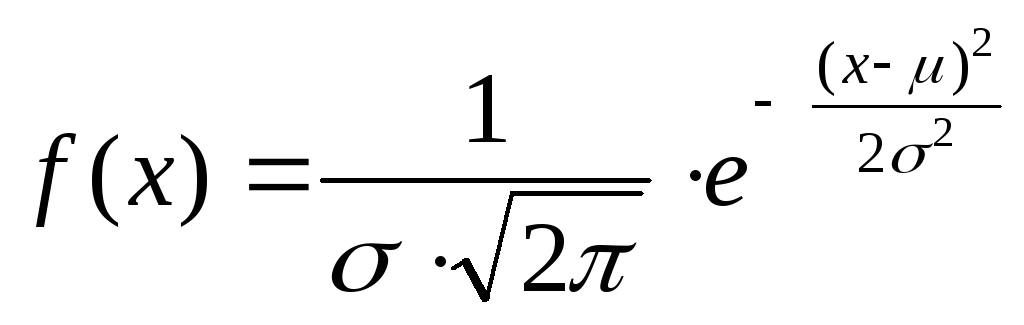 , (4)
, (4)
где - выборочное среднее, σ – среднее квадратическое отклонение;
Тогда :
, (5)
Затем, с помощью критерия Пирсона сравним эмпирические ( ) и теоретические (
) частоты:
По таблице критических точек распределения с заданным уровнем значимости
и числу степеней свободы
находим критическую точку правосторонней критической области
. Так как
, то гипотезу о нормальном распределении генеральной совокупности отвергаем.
Аналогично, с помощью данной программы, можно провести статистическую обработку и других данных с пробной площади из инвентаризационной ведомости (высоты деревьев (h, м), диаметра на высоте
Проведённые исследования (расчёты)с использованием ППП Mathcadпозволяют вывести следующие результаты, дать практические рекомендации и выводы.
Результаты анализа данной выборки диаметров клёна остролистного (AcerplatanoidesL.) на высоте 1,3 м:
– выборочная средняя измерений деревьев по диаметру составляет 27,1 см;
– изменчивость диаметра клёна остролистного характеризуется средним квадратическим отклонением, которое для выборочной совокупности составляет см, коэффициент вариации равен
, что говорит о значительной изменчивости деревьев по диаметру и подтверждается опытными данными. Проанализировав интервальный ряд распределения выборки, видим, что для улучшения полученных результатов можно отбросить нехарактерные данные, т.е. последний интервал (таблица 2), объединить с предпоследними, что позволит уменьшить среднее квадратическоеотклонение и коэффициент вариации. Диаметр у деревьев клёна, посаженных в один вегетационный период сильно варьируется, возможно, это связано с климатическими условиями, приживаемостью деревьев и другими факторами, которые влияют на рост и развитие насаждений;
– оценка достоверности основных статистических показателей приводит к выводу о надёжности выборочной средней, среднего квадратическогоотклонения, коэффициента вариации и асимметрии на 5%-ном уровне значимости. В то же время такой показатель, как эксцесс, характеризующий крутость эмпирической кривой, недостоверен, что позволяет считать его практически отсутствующим;
– на основании проверки критерия согласия Пирсона мы приходим к выводу о том, что измерения деревьев по диаметру нельзя считать распределенными по нормальному закону. Это можно объяснить недостаточным объёмом выборки и наличием нехарактерных показателей.
Главные выводы проделанной работыс использованием ППП Mathcadсостоят в том, что были показаны последовательные и подробные этапы математической обработки результатов лесокультурных исследований, расчёт основных статистических показателей (выборочная средняя измерений деревьев по диаметру, выборочная дисперсия, среднее квадратическое отклонение, коэффициент вариации иасимметрии на 5%-ном уровне значимости) и их оценка (оценка достоверности основных статистических показателей). ППП Mathcadпозволяет оперировать большим числом данных, быстро и с достаточной точностью обрабатывать и сравнивать результаты измерений,полученных при подеревной инвентаризации в лесном хозяйстве, поэтому данную программу можно внедрять в производство, в работе на конкретных примерах пошагово представили действия и расчёты для получения основных статистических показателей, применительно к лесокультурным исследованиям.
1. Барышникова, Е.В. Математика. Математическая статистика [Текст]: метод. указания к выполнению расчётно-графической работы для студентов всех специальностей / Е.В.Барышникова; Фед. гос. бюджетное образоват. учреждение высш. проф. образования «Новочеркасская гос. мелиор. акад.», каф. математики.- Новочеркасск, 2010.- 61 с.
2. Гмурман, В.Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов [Текст]: учеб. пособие для вузов- 9-е изд., стер. Книги Математика /В.Е. Гмурман.- М.: Высшая школа, 2003. - 479 с. EDN: https://elibrary.ru/QJLKXP
3. ГОСТ 16483.6-80 (СТ СЭВ 1141-78). Древесина. Метод отбора модельных деревьев и кряжей для определения физико-механических свойств древесины насаждений. - Введ. 1981-01-01 [Текст]. - М.: Стандартинформ, 2005. - 6 с.
4. Доспехов, Б. А. Методика полевого опыта (с основами статистической обработки результатов исследований) [Текст] / Б.А. Доспехов. - 5-е изд., доп. и перераб. - М.: Агропромиздат, 1985. - 351 с., ил.
5. Зайцев, Г.Н. Математическая статистика в экспериментальной ботанике [текст] / Г.Н. Зайцев. - М.: Изд. Наука, 1984. - 424 с.
6. Ивонин, В.М. Лесомелиорация ландшафтов.Научные исследования [текст] / В.М. Ивонин, Н.Д. Пеньковский. - Ростов-на-Дону, 2003. - 152 с.
7. Карта г. Новочеркасска (Шахтинское шоссе) [Электронный ресурс]. - режим доступа: https://www.google.com/maps/@47.5039335,40.1025466,1514m/data=!3m1!1e3?hl=ru-RU. - Загл. с экрана.
8. Кох, Е.В. Вертикальная структура фитомассы в сосняках искусственного происхождения [Текст]: автореф. … канд. с.-х. наук: 06.03.02/ Е.В. Кох. - Екатеринбург, 2013. - 24с. EDN: https://elibrary.ru/SVCYZJ
9. Кочегурова, Е.А. Основы работы и программирования в системе Mathcad [Текст]: учеб. пособие / Е.А. Кочегурова. -Томск, 2012. - 25 с.
10. Кружилин, С.Н. Рост дуба черешчатого в лесных культурах, созданных с применением разных типов смешения в условиях Нижнего Дона [Текст]: автореф. … канд. с.-х. наук: 06.03.01/ С.Н. Кружилин. - Брянск, 2008. - 25с. EDN: https://elibrary.ru/NJJIBJ
11. Медведева, Е.Ю. Биолого-экологические особенности роста и размножения гибридных тополей в городе Екатеринбурге [Текст]: дис. … канд. с.-х. наук: 06.03.03: защищена 07.10.2015 / Е.Ю. Медведева. - Екатеринбург, 2015. - 210 с. - Библиогр.: с. 166-187. EDN: https://elibrary.ru/EORHYK
12. Митропольский, А.К. Техника статистических вычислений [Текст]: 2-е изд., перераб. и доп. серия «Физико-математическая библиотека инженера» /А.К. Митропольский. - М.: Наука, 1971. - 576 с. : ил.
13. Приказ Министерства образования и науки Российской Федерации №1027 от 23 октября 2017 года (ред. от 23.03.2018) «Об утверждении номенклатуры специальностей, по которым присуждаются ученые степени» [Электронный ресурс] // информационно-правовой портал ГАРАНТ.РУ. - Режим доступа: https://www.garant.ru/products/ipo/prime/doc/71714408/.
14. Танюкевич,В.В. Эколого-мелиоративное состояние осокорников в условиях загрязнения Доно-Аксайской поймы [Текст]: дис. ... канд. с.-х. наук: 03.00.16: защищена 10.12.2004 / В.В. Танюкевич. - Новочеркасск, 2004. - 225 c. - Библиогр.: с 182-201. EDN: https://elibrary.ru/NMYAVT
15. Knibbeler, V.•Higher-Dimensional Automorphic Lie Algebras Lombardo [Text] / V. Knibbeler, S.•Lombardo, Jan A. Sanders // The Journal of the Society for the Foundations of Computational Mathematics. - 2017. - Vol. 17, no4. - pp. 987-1035. DOIhttps://doi.org/10.1007/s10208-016-9312-1. EDN: https://elibrary.ru/TVGNUE
16. McNeill,J.Major changes to the Code of Nomenclature - Melbourne, July 2011[Text] / J. McNeill, N.J. Turland // Taxon. -2011. -Vol. 60, no. 4 - pp. 1495-1497.
17. Pearsall, D.M. Encyclopedia of Archaeology[Text] / D.M. Pearsall. - San Diego, Calif. : ElsevierAcademic Press, 2008. - 2382 p. EDN: https://elibrary.ru/QPRAIN
18. Warne, R. Statistical Methods Used in Gifted Education Journals, 2006-2010 [Text] / R. Warne, M. Lazo, T. Ramos, and N. Ritter // Gifted Child Quarterly. -2012. - Vol. 56, no 3. - pp. 134-149. doi:https://doi.org/10.1177/0016986212444122.
19. White, C. Unkind cuts at statisticians [Text] / C. White //The American Statistician. - 1964. - Vol. 18, no. 5. - pp. 15-17.












