Москва, г. Москва и Московская область, Россия
Москва, г. Москва и Московская область, Россия
УДК 37 Образование. Воспитание. Обучение. Организация досуга
Обоснована необходимость включения дифференциальных уравнений и простейших дифференциальных моделей в математическую подготовку будущего бакалавра менеджмента. Анализируются возможности Wolfram-технологий в контексте преподавания учебной темы «Дифференциальные уравнения» для будущих бакалавров менеджмента. Представлены дидактические условия повышения качества математической подготовки будущего бакалавра менеджмента в современных условиях сокращения часов на аудиторную работу. Установлена связь прикладного усиления обучения элементам высшей математики с развитием инновационных компонентов профессиональной компетентности будущего бакалавра менеджмента, связанных с управлением и принятием решений в условиях риска, неопределенности и неполноты информации. В рамках темы исследования спроектировна система микроцелей, в полной мере описывающая учебно-познавательную деятельность студентов и поддерживающая методически обоснованное включение Wolfram-технологий. Представленные рекомендации и примеры использования нового инструментального средства WolframAlpha позволяют отказаться от спонтанной и фрагментарной реализации принципа информатизации учебного процесса, позволяют по-новому организовать учебно-познавательную деятельность студента. Результаты, изложенные в данной статье, могут быть полезны для педагогов, преподавателей математических дисциплин, разработчиков программного обеспечения и электронных образовательных ресурсов, интересующихся современными подходами к повышению качества профессиональной подготовки выпускников вузов.
Wolfram, дифференциальные уравнения, дифференциальная модель, моделирование, бакалавр менеджмента, информатизация, прикладная направленность.
Введение. Вопросы включения элементов теории дифференциальных уравнений, а также механизмов построения и исследования простейших дифференциальных моделей в математическую подготовку будущих бакалавров менеджмента представляют особый интерес в контексте усиления прикладной направленности обучения. В качестве важнейшей задачи профессиональной подготовки будущего бакалавра менеджмента в университете отметим задачу подготовки выпускника, соответствующего новым требованиям цифровой экономики. Инструментальной основой достижения этой непростой цели может выступать компетентностный подход [5], аппарат педагогического проектирования и теория педагогических технологий [6, 8]. Их использование в Институте цифровой экономики и информационных технологий в практике преподавания ряда математических дисциплин («Высшая математика», «Теория вероятностей и математическая статистика», «Методы оптимальных решений», «Теория оптимального управления») способствует созданию дидактических условий для подготовки будущих бакалавров менеджмента в соответствии с требованиями динамично развивающегося рынка труда.
Содержательно-методические аспекты прикладного усиления математической подготовки будущего бакалавра менеджмента. В современных условиях математизации и информатизации систем управления будущий бакалавр менеджмента должен демонстрировать высокие показатели эффективности работы с математическими и имитационными моделями управления, новыми инструментальными средствами поддержки принятия решений, а также иметь необходимый уровень адаптации к меняющимся социально-экономическим условиям. Отметим, что изменение социально-экономических условий, усложнение социальных, политических отношений, а также активное внедрение информационных технологий в исследования в области управления, неравномерный переход регионов России к инновационной экономике требуют изменения технологий подготовки будущих бакалавров менеджмента. Важно понимать, что важнейшим условием достижения поставленных задач в области повышения качества профессиональной подготовки будущего бакалавра менеджмента является реализация усиления прикладной (профессиональной) составляющей обучения. Мы придерживаемся точки зрения, что принцип усиления прикладной направленности обучения математическим дисциплинам должен быть распространен на все виды учебно-познавательной деятельности студентов. При этом перспективным нам представляется раскрытие потенциала интеграции информационных и педагогических технологий.
Исследователи, интересующиеся проблематикой совершенствования преподавания математических дисциплин, отмечают изменение роли и востребованности математического языка, математического аппарата, математических методов [2, 15, 16] в рамках системы подготовки студентов в университете, в том числе и будущих бакалавров менеджмента. Так по существу математика перестаёт быть общей развивающей дисциплиной и приобретает роль важной инструментальной составляющей, необходимой для последующего изучения многих профессиональных учебных дисциплин.
Роль информационных технологий в условиях реализации прикладной направленности обучения математике в вузе раскрыта в исследованиях [1, 14]. Мы согласны с авторами, что особую роль приобретает реализация межпредметных связей, которая невозможна без многоуровневой интеграции информационных и педагогических технологий. Как показывает практика опытно-экспериментальной работы со студентами Российского экономического университета им. Г. В. Плеханова, практическая реализация компетентностного подхода и элементов теории педагогических технологий в рамках математической подготовки будущего бакалавра менеджмента предполагает разработку новых методик и технологических материалов для обеспечения более тесного и целенаправленного взаимодействия математики с такими проблемными областями как теория оптимального управления и экономический анализ. Математический аппарат является основой устойчивого развития социально-экономических систем, а также основой управления инновациями, управления качеством, управления изменениями, управления проектами и так далее.
С нашей точки зрения доминирующей целью математической подготовки будущих бакалавров менеджмента является выработка компетенции в области применения современных математических методов исследования социально-экономических ситуаций, предполагающих оптимальное управление. При проектировании методических систем обучения математическим дисциплинам будущего бакалавра менеджмента необходимо учитывать, что математический язык является универсальным языком описания управленческих систем и процессов. Именно базу для представлений о роли математического моделирования, а также возможности для проведения простейших исследований предоставляет учебный курс «Высшая математика», традиционно изучаемый студентами бакалавриата менеджмента на рамках первого года обучения в университете.
Отметим, что возрастает роль преподавателя математических дисциплин в бакалавриате. Без освоения базовых математических понятий и категорий («Число», «Вектор», «Матрица», «Отношение», «Операция», «Функция», «Производная», «Интеграл», «Уравнение», «Неравенство», «Система», «Линия уровня», «Модель», «Вероятность» и т.д.) невозможно дальнейшее решение профессиональных задач, связанных с принятием решений в условиях неопределённости, риска и неполноты информации. Перечисленные математические понятия связаны с выбором оптимальных программ развития, совершенствованием систем управления.
Естественным образом возникает необходимость направленного обучения студентов бакалавров менеджмента решению прикладных математических задач, охватывающих различные ситуации и проблемы управленческой деятельности. Эти прикладные математические задачи позволяют на необходимом уровне иллюстрировать возможности и приложения математики в рамках будущей профессиональной деятельности. Мы придерживайся точки зрения, что учебная дисциплина «Высшая математика» должна быть направлена не только на знакомство с теоретическим материалом, на решение традиционных, классических задач, но и направлена на формирование компетенций в области практического применения математических знаний к решению прикладных задач, связанных с оптимальным управлением.
Принципы проектирования учебных курсов в условиях информатизации образования, представленные в исследованиях [9, 12] предполагают создание специальных научно-методических материалов, в содержании которых отражено тесное взаимодействие математики и других предметных областей. Таким образом, первостепенной целью математической подготовки студентов будущих бакалавров менеджмента является выработка компетенций в области применения современных методов исследования, основу которых составляют количественные методы и математическая моделирование.
Содержание и методы решения профессиональных задач, с которыми сталкивается будущий бакалавр менеджмента, требуют успешного освоения содержания базовой учебной дисциплины «Высшая математика». Следовательно, возникает необходимость обучения студентов решению прикладных задач, в полной мере демонстрирующих прикладные возможности современного математического аппарата в будущей профессиональной деятельности, связанный с анализом управленческих ситуаций и выбором оптимального плана управления.
Основы классического подхода к обучению студентов бакалавриата менеджмента составляют изучение теории и решение задач, требующих знание теоретического материала. Как правило, программный материал сопровождается решением достаточно абстрактных задач (например, задач на физический и механический смысл производной, задач на моделирование физических явлений на основе дифференциальных уравнений). Естественно, что такой подход в целом адекватен истории развития математики как науки. Однако практика подготовки будущего бакалавра менеджмента в современных условиях требует изменения подходов к обучению высшей математике. Новые компетенции в области применения математики, а также интеграция математических методов с новым инструментальными средствами, например, WolframAlpha [3, 10, 11], становится важным компонентом профессиональной подготовки будущих бакалавров менеджмента. Выпускники бакалавриата менеджмента должны быть готовы к использованию математики и инструментальных средств к решению задач повышения качества управления.
Прикладное усиление математической подготовки будущего бакалавра менеджмента на уровне учебной темы «Дифференциальные уравнения».
В описанных условиях возрастает значение теории дифференциальных уравнений и соответственно учебной темы «Дифференциальные уравнения». Как известно дифференциальные уравнения описывают связь между неизвестной функцией с её производными. В практике принятия решений достаточно широко находят использование дифференциальные модели, однако в практике математической подготовки будущего бакалавра менеджмента в университетах к настоящему времени они представлены недостаточно.
Практика преподавания математических дисциплин свидетельствует, что используемые в экономических исследованиях дифференциальные модели требуют содержательно-методической адаптации для включения в содержание математических дисциплин для подготовки будущего бакалавра менеджмента. Как правило, дифференциальные уравнения в контексте экономических приложений используются для описания макроэкономических проблем и ситуаций [7]. С другой стороны, использование дифференциальных уравнений позволяет описывать, моделировать различные процессы, происходящие как на микро, так и на макроуровне. Важно отметить, что дифференциальные уравнения направлены на описание динамики экономической, управленческой ситуации [13]. По существу, в рамках дифференциального уравнения исследуются взаимосвязь между переменными в контексте времени [4]. Применение специально разработанного механизма, называемого начальными условиями, в процессе построения дифференциальных моделей позволяет исследователям получать сведения о начальном и перспективном состояниях исследуемого управленческого процесса, проанализировать её развитие и прогнозировать развитие ситуации.
Выделим далее наиболее актуальные вопросы в области «Оптимальное управление» для применения аппарата дифференциальных уравнений.
Направление I. «Управление на основе анализа взаимосвязи спроса и предложения».
Направление II. «Управление на основе взаимосвязи функции спроса и стоимости».
Направление III. «Моделирование процесса формирования равновесной цены на производимую продукцию».
Направление IV. «Моделирование естественного роста и управление на основе влияния естественного роста».
Направление V. «Управление на основе исследования эффективности рекламы».
Направление VI. «Управление на основе анализа дохода и потребления».
Направление VII. «Управление на основе на основе анализа инфляционного ожидания».
Направление VIII. «Управление на основе моделирования рынка спрогнозированы ценными».
Направление IX. «Управление на основе модели хищник жертва».
Более подробно в рамках данной статьи остановимся на девятом направлении. Традиционно дифференциальная модель «Хищник-жертва» служит для описания межвидовой конкуренции в биолого-математических исследованиях. Эта модель, часто называемая моделью Лоттки-Вольтерра является математической моделью взаимодействия между представителями двух биологических видов, находящимися в определенных отношениях, таких как «хищник-жертва», «паразит-хозяин» и т.д. С математической точки зрения моделируется межвидовая конкуренция биологических видов системой двух дифференциальных уравнений.
В общем виде дифференциальная модель «Хищник-жертва» представляется следующей системой:

Обратим внимание, что оба дифференциальных уравнений являются уравнениями первого порядка. В данной дифференциальной модели количество «жертв» будет задано функцией x=x(t), количество «хищников» задано функцией y=y(t). Предполагается, что x0=x(t0) жертв и y0=y(t0) взаимодействуют в рамках некоторой закрытой биологической системы в момент времени t0.
Важно понимать, что важный прикладной аспект дифференциальных моделей заключается в изучении нелинейной динамики [13]. В частности, согласно предпосылкам модели «Хищник-жертва», значения величин х и у характеризуются колебаниями. Увеличение числа потенциальных жертв способствует увеличению количества хищников, что в свою очередь приводит к уменьшению числа жертв, за счет чего в последствии уменьшается число хищников и т. д. Таким образом процесс межвидовой конкуренции носит циклический характер. Его можно визуализировать следующим образом: точка на плоскости с координатами (x, y) совершает движение вдоль некоторой замкнутой фазовой траектории вокруг особой точки (точки равновесия). Расположение точки равновесия зависит от особенностей конкретной ситуации, в частности выраженных в виде параметров дифференциальной модели.
Проведение численного эксперимента на основе модели «Хищник-жертва» позволяет исследователю установить закономерности, имеющие принципиальное значения для понимания ситуации и количественно описывающие поведение биологической системы. Задаче выявления закономерностей и описания поведения биологической системы служит понятие «Равновесие системы», а также понятие «Фазовая траектория» (фазовый портрет). Эти понятия являются достаточно сложными как с содержательной, так и с вычислительной точек зрения. Их неформальное включение в математическую подготовку будущего бакалавра менеджмента требует применения новых инструментальных средств и информационных технологий. Мы считаем, что таким новым инструментальным средством может выступать база знаний и набор вычислительных алгоритмов WolframAlpha.
Инструментальное средство WolframAlpha в организации учебно-познавательной деятельности студентов на уровне учебной темы «Дифференциальные уравнения». Первой инструментальной возможностью WolframAlpha для организации учебно-познавательной деятельности студентов является непосредственное решение дифференциального уравнения или системы дифференциальных уравнений. С этой целью необходимо использовать запрос «Solve». Отметим, что для нахождения решения дифференциальное уравнение или система дифференциальных уравнений должны быть заданы конкретными числовыми параметрами.

Рисунок 1. Результат реализации запроса Solve.
На рис. 1 представлен результат реализации запроса Solve для исследования дифференциальной модели. Однако даже после получения решения дифференциального уравнения или системы дифференциальных уравнений, требуются еще значительные усилия для исследования полученного решения. Другими словами, сразу интерпретировать полученное решение не представляется возможным – необходимо дополнительное исследование.
Второй инструментальной возможностью WolframAlpha является специально созданная процедура, запускаемая по запросу «Predator-prey model». Пример реализации этой возможности представлен на рис. 2.

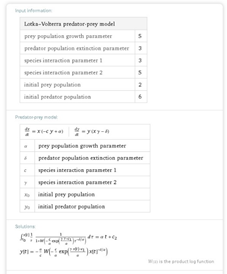

Рисунок 2. Результат реализации исследования модели Хищник-Жертва на основе процедуры «Predator-prey model».
В содержании математической подготовки будущего бакалавра менеджмента должны быть отражены различные аспекты математического моделирования, продемонстрировано что моделирование является универсальным методом познания. Так, ряд биологических и экономических процессов подчинены общим закономерностям и количественно описываются моделями в виде дифференциальных уравнений. В частности, одинаковый математический аппарат может быть использован для исследования динамики кадрового состава между секторами и динамики биологических масс в борьбе за выживание.
Имеющиеся к настоящему времени исследования по нелинейной экономической динамики и применению дифференциальных уравнений в экономических исследования подводит к необходимости совершенствования содержания математической подготовки будущего менеджера. Одной из методически значимых задач, связанных с повышением качества математической подготовки будущего бакалавра экономики, является переосмысление связей классической модели «Хищник-жертва» с другими построениями теории дифференциальных уравнений. Уточнение данных связей и отражение их в практике подготовки будущего менеджера позволит понять механизмы перехода модели «Хищник-жертва» в другие формальные конструкции. Мы считаем, что необходимо проведение логико-методического анализа связей классической модели «Хищник-жертва» с такими объектами и понятиями, как «Логистическое уравнение», «Уравнение Я. Риккати», «Уравнение второй степени Я. Бернулли» и «Дифференциально-разностное уравнение Полтеровича-Хенкина». Таким образом, одной из задач прикладной математической подготовки будущего бакалавра менеджмента нам представляется демонстрация внутреннего единства и непротиворечивости разнообразных количественных инструментов при моделировании биологических, социально-экономических и управленческих проблем и ситуаций.
В завершение статьи сформулируем шесть микроцелей, позволяющих в полной мере описать учебно-познавательную деятельность студента в рамках учебной темы «Дифференциальные уравнения» и поддерживающих интеграцию информационных и педагогических технологий как условие реализации прикладной направленности профессиональной подготовки.
Микроцель 1. Понимание множества ситуаций, приводящих к классической модели «Хищник-жертва».
Микроцель 2. Осознание необходимости записи исследуемой ситуации в виде системы нелинейных дифференциальных уравнений.
Микроцель 3. Знание сущности параметров дифференциальной модели:
- параметр 1 – «Коэффициент прироста количества жертв»
- параметр 2 – «Коэффициент убывания хищников»
- параметр 3 – «Коэффициент поедания жертв хищниками» (межвидовое взаимодействие первого типа);
- параметр 4 – «Коэффициент рождаемости хищников» (межвидовое взаимодействие второго типа);
- параметр 5 – «Величина начального числа жертв в популяции» (начальное условие первого типа);
- параметр 5 – «Величина начального числа хищников в популяции» (начальное условие второго типа).
Микроцель 4. Задание численных значений параметров дифференциальной модели.
Микроцель 5. Понимание вида результата исследования дифференциальной модели:
- общее решение системы;
- точка равновесия системы;
- семейство фазовых траекторий системы (фазовый портрет).
Микроцель 6. Содержательная интерпретация полученного результата в терминах рассматриваемой ситуации.
Выводы. В процессе работы уточнена роль дифференциальных уравнений и простейших дифференциальных моделей в контексте развития профессиональной компетентности будущего бакалавра менеджмента. Раскрыты современные компоненты профессиональной компетентности будущего бакалавра менеджмента с учетом математизации и информатизации управленческих исследований, тенденции к повышению требований к уровню прикладной математической подготовки будущего бакалавра менеджмента. Обоснована необходимость практической реализации принципа усиления прикладной направленности обучения элементам высшей математики, инструментальной основой которой выступает новое инструментальное средство WolframAlpha.
1. Асланов Р. М., Игнатова О. Г. Электронное обучение вчера, сегодня, завтра. Проблемы и перспективы // Continuum. Математика. Информатика. Образование. - 2018. - № 1 (9). - С. 28-35.
2. Власов Д. А. Методика количественного анализа при принятии решений в различных информационных условиях // Системные технологии. - 2018. - № 4 (29). - С. 18-29.
3. Власов Д. А., Синчуков А. В. Новые технологии Wolframalpha в контексте исследования проблем новой экономики//Конкурентоспособность в глобальном мире: экономика, наука, технологии. - 2017. - № 5-5 (47). - С. 20-24.
4. Геворкян Э. А., Синчуков А. В., Татарников О. В. Динамика изменения национального дохода в рамках модели гармонического осциллятора // Фундаментальные исследования. - 2018. - № 10. - С. 26-30.
5. Зверева А. И. Совершенствование технологий преподавания высшей математики для студентов экономического университета / В сборнике: Управление региональным развитием: проблемы, возможности, перспективы развития Сборник научных статей по материалам Международной научно-практической конференции с международным участием. Ответственный редактор Е.А. Ильина. - 2018. - С. 191-195.
6. Карасев П. А., Чайковская Л. А. Совершенствование программ высшего образования в контексте современных требований рынков образовательных услуг и профессионального сообщества // Экономика и управление: проблемы, решения. - 2017. - Т. 3. - № 2. - С. 3-9.
7. Лихачев Г. Г., Сухорукова И. В. Компьютерное моделирование и математическое обеспечение экономико-социальных задач // Экономический анализ: теория и практика. - 2003. - № 5 (8). - С. 60-62.
8. Монахов В. М. Дидактическая аксиоматика когнитивной теории педагогических технологий /В. М. Монахов//Современные информационные технологии и ИТ-образование. - 2016. - Т. 12. - № 3-1. - С. 32-39.
9. Муханов С. А. Использование информационных технологий для индивидуализации обучения математике на примере темы «Дифференциальные уравнения» / С. А. Муханов, А. А. Муханова, А. И. Нижников // Вестник Московского городского педагогического университета. Серия: Информатика и информатизация образования. - 2018. - № 1 (43). - С. 72-77.
10. Муханов С. А., Бритвина В. В., Муханова А. А. Использование технологии Wolfram CDF при изучении нелинейных колебаний // Системные технологии. - 2018. - № 1 (26). - С. 23-26.
11. Муханов С. А., Муханова А. А. Использование сервиса Wolfram|Alpha при моделировании вероятностных экспериментов // Современное педагогическое образование. - 2019. - № 2. - С. 67-69.
12. Муханов С. А., Нижников А. И. Проектирование учебного курса // Педагогическая информатика. - 2014. - № 4. - С. 39-46.
13. Петров Л. Ф. Методы нелинейной динамики как инструменты управления экономической эффективностью // Эффективное антикризисное управление. - № 2. - 2011. - С. 58-67.
14. Синчуков А. В. Роль информационных технологий в совершенствовании подготовки бакалавра менеджмента // Continuum. Математика. Информатика. Образование. - 2018. - № 2 (10). - С. 121-127.
15. Тихомиров Н. П., Тихомирова Т. М. Риск-анализ в экономике. - М.: ЗАО «Издательство «Экономика», 2010. - 318 с.
16. Тихомиров Н. П., Тихомирова Т. М. Совершенствование управления природоохранной деятельностью на территориях экологически опасных объектов // Экономика природопользования. - 2000. - № 1. - С. 33-45.













