с 01.10.2008 по настоящее время
Россия
В 2016 г. в издательстве ИНФРА-М вышла монография «Циклида Дюпена и ее приложение», в которой исследуется поверхность, образованная двумя семействами окружностей и названная циклидой Дюпена в честь открывшего ее великого французского ученого Пьера Шарля Франсуа Дюпена, ученика Гаспара Монжа. В монографии рассматриваются свойства циклиды Дюпена, ее приложение к различным геометрическим построениям, а также возможность практического применения в технике, архитектуре и учебном процессе.
циклида Дюпена, коники, задача Аполлония, задача Ферма, геометрические построения, архитектурные оболочки
В учебном курсе начертательной геометрии для студентов вузов изучается класс поверхностей, образованный окружностями и названный «Циклические поверхности» [3; 6; 9; 10]. Внутри этого класса поверхностей есть так называемые каналовые поверхности. Циклиды Дюпена принадлежат к каналовым поверхностям, более того - они являются частным случаем [1; 2; 7; 8] этих поверхностей, но в курсе начертательной геометрии их формирование не рассматривается. В учебном курсе инженерной графики изучается ряд сопряжений, но опять-таки не упоминается о циклидах Дюпена [4; 13, 14], хотя, прочитав данную книгу, можно убедиться, что все построения сопряжений основаны на свойствах циклиды Дюпена.
Циклиды Дюпена были открыты Пьером Шарлем Франсуа Дюпеном [5; 11] в начале XIX в. и названы в его честь. Сам Дюпен был учеником Гаспара Монжа, как и многие великие ученые Франции того времени.
Циклиды Дюпена обычно представляются как огибающие семейства сфер, касающихся трех заданных [5; 7; 8]. Общеизвестная поверхность тор - это частный случай циклид Дюпена. Еще более частные случаи - конусы и цилиндры вращения [5].
О фокальной поверхности. Если к некоторой поверхности провести нормаль, то центры окружностей главных кривизн на этой нормали дадут две точки. Два множества этих точек при перемещении нормали по поверхности создают две фокальные поверхности. Циклиды - это единственные поверхности, у которых фокальные поверхности вырождаются в линии, а все линии кривизны являются окружностями.
Монография состоит из двух разделов. В первом разделе описываются свойства циклид Дюпена, во втором - их приложение.
К основным свойствам циклид Дюпена относятся следующие:
- Задание трех сфер определяет в пространстве положение четырех циклид Дюпена.
- Сечение циклиды Дюпена и данных трех сфер их общей плоскостью симметрии представляет собой два из восьми возможных решений задачи Аполлония.
- Множество центров касательных сфер (вырожденная фокальная поверхность) расположены в плоскости, являющейся плоскостью симметрии циклиды Дюпена, и представляют собой в общем случае кривую второго порядка.
- Линия касания циклиды с вписанной в нее сферой представляет окружность (одну из линий кривизны), плоскость которой перпендикулярна их общей плоскости симметрии.
- Три конуса вращения, вершинами которых являются центры трех заданных сфер, а направляющими - окружности касания, принадлежащие этим сферам, имеют одну общую плоскую линию пересечения - кривую второго порядка, которой принадлежат центры всего множества сфер, касательных к трем данным сферам. Эту кривую можно рассматривать как результат сечения любого из отмеченных выше трех конусов основной плоскостью симметрии Δо (Рис. 1) циклиды Дюпена, огибающей данные сферы.

Рис. 1. Две проекции циклиды Дюпена
6. Плоскость, которой принадлежит линия центров множества сфер, касательных трем данным сферам, и плоскости трех окружностей касания, принадлежащих данным сферам, пересекаются по одной прямой - по оси циклиды Дюпена. См. уравнения (1), (2). Следовательно, все плоскости окружностей касания любых вписанных в циклиду Дюпена сфер будут пересекаться по оси циклиды.

Другими словами, если даны три сферы, то плоскость линии центров множества касательных к ним сфер и плоскости окружностей касания являются пучком плоскостей.
7. Если провести две плоскости, каждая из которых касается циклиды Дюпена по окружности, то центры этих двух окружностей касания определяют положение оси циклиды Дюпена.
8. Если даны две произвольные сферы, то оси всего множества циклид Дюпена, огибающих эти сферы, будут принадлежать плоскости, перпендикулярной оси конуса, касательного к этим сферам и проходящей через середину расстояния между плоскостями окружностей касания.
9. Если даны две произвольные сферы, то ось огибающей их произвольной циклиды Дюпена будет принадлежать плоскости, перпендикулярной линии центров этих сфер и пересекающей эту линию в точке, удаленной от центра первой сферы на расстояние, равное сумме половины расстояния между центрами сфер и отношения разности величин радиусов первой и второй сферы к удвоенному расстоянию между центрами - формула (3).
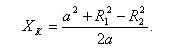
Далее показывается, что фокальными линиями являются кривые второго порядка (коники). Показывается, что, если имеем софокусные коники, то имеется множество конусов вращения, вершины которых принадлежат одной конике, а линия их пересечения - софокусная коника.
Приводится новое конструирование гиперболических поверхностей.
Во втором разделе показываются новые классические решения (с помощью циркуля и линейки) знаменитой задачи Аполлония о касании трех заданных окружностей четвертой.
Далее рассматриваются все случаи решения задач на сопряжение прямых и окружностей [11; 14], применяемых в архитектуре и других областях. При этом доказывается, что все известные приемы - это, по сути, частные случаи применения свойств циклид Дюпена.
Классическая задача Ферма о касании четырех сфер пятой также рассматривается с точки зрения применения свойств циклид Дюпена. Эта задача может быть применена при решении проблем плотной укладки.
Затем рассматриваются все возможные способы построения кривых второго порядка. Эти способы могут быть применены в компьютерных технологиях для пока что незаложенного способа построения гипербол и парабол в графические системы.
Кроме самих коник [11; 12] могут быть построены касательные и нормали [11; 15] к ним, а также эквидистантные кривые.
Далее рассматриваются переходные элементы трубопроводов, а также применение отсеков циклид Дюпена для архитектурных сооружений.
В конце монографии [11] приводятся примеры использования частных случаев циклид Дюпена в учебном процессе на факультете «Архитектура» Московского государственного академического художественного института имени В.И. Сурикова.
1. Берже М. Геометрия. Т.1 [Текст] / М. Берже. - М.: Мир, 1984. - 500 с.
2. Берже М. Геометрия. Т.2 [Текст] / М. Берже. - М.: Мир, 1984. - 368 с.
3. Бубенников А.В. Начертательная геометрия [Текст] / А.В. Бубенников, М.Я. Громов. - М.: Высшая школа, 1973.
4. Вышнепольский В.И., Сальков Н.А. Цели и методы обучения графическим дисциплинам [Текст] / В.И. Вышнепольский, Н.А. Сальков // Геометрия и графика. - 2013. - Т. 1. - № 2. - С. 8-9. - DOI:https://doi.org/10.12737/777.
5. Гильберт Д. Наглядная геометрия [Текст] / Д. Гильберт, С. Кон-Фоссен. - М.-Л.: Объединенное научно-техническое издательство НКТП СССР, Главная редакция общетехнической литературы и номографии, 1936. - 302 с.
6. Иванов Г.С. Начертательная геометрия: учебник [Текст] / Г.С. Иванов. - М.: ФГБОУ ВПО МГУЛ, 2012. - 340 с.
7. Клейн Ф. Высшая геометрия [Текст] / Ф. Клейн. - М.-Л.: ГОНТИ, 1939. - 400 с.
8. Кривошапко С.Н. Энциклопедия аналитических поверхностей [Текст] / С.Н. Кривошапко, В.Н. Иванов. - М.: Книжный дом «ЛИБРОКОМ», 2010. - 560 с.
9. Сальков Н.А. Начертательная геометрия: базовый курс: учеб. пособие [Текст] / Н.А. Сальков. - М.: ИНФРА-М, 2013. - 184 с.
10. Рыжов Н.Н. Начертательная геометрия: понятия, их определения и пояснения [Текст] / Н.Н. Рыжов. - М.: МАДИ, 1993. - 60 с.
11. Сальков Н.А. Циклида Дюпена и ее приложение [Текст] / Н.А. Сальков. - М.: ИНФРА -М, 2016. - 145 с.
12. Сальков Н.А. Циклида Дюпена и кривые второго порядка. Часть 1 [Текст] / Н.А. Сальков // Геометрия и графика. - 2016. - Т. 4. - № 2. - С. 19-28. - DOI:https://doi.org/10.12737/.
13. Сальков Н.А. Проблемы современного геометрического образования [Текст] / Н.А. Сальков // Проблемы качества графической подготовки студентов в техническом вузе: традиции и инновации. - 2014. - Т. 1. - С. 38-46.
14. Сальков Н.А. Черчение для слушателей подготовительных курсов [Текст] / Н.А. Сальков. - М.: ИНФРА-М, 2016. - 128 с.
15. Сальков Н.А. Эллипс: касательная и нормаль [Текст] / Н.А. Сальков // Геометрия и графика. - 2013. - Т. 1. - № 1. - С. 35-37. - DOI:https://doi.org/10.12737/2084.






