Московский государственный университет им. М.В. Ломоносова (кафедра социокультурного проектирования и развития территорий, профессор)
Москва, г. Москва и Московская область, Россия
Россия
Представлена авторская классификация научно-практических методов принятия управленческих решений по признаку применения в прикладных областях менеджмента. Дана общая характеристика методов принятия управленческих решений на основе детерминированного факторного анализа. Описано содержание, области применения, достоинства и недостатки методов принятия управленческих решений на основе детерминированного факторного анализа, включая методы: цепных подстановок, индексный, абсолютных разниц, относительных разниц, пропорционального деления, дифференциального исчисления, простого прибавления неразложимого остатка, взвешенных конечных разностей, логарифмический, коэффициентов, интегральный.
методы, принятие управленческих решений, детерминированный факторный анализ.
Чем глубже человек проникает в сущность изучаемых явлений, тем более точные методы исследования ему требуются и тем более рациональные варианты решений он получает [1, с. 245–246].
Проведенный анализ вариантов классификации научно-практических методов принятия решений показал [2], что наибольший интерес представляет анализ классификации методов ПУР по способам принятия решений, где выделяются:
• методы, построенные на интуиции управляющего, на его ранее накопленном опыте и сумме знаний в конкретной области деятельности;
•методы, сформированные на понятии «здравый смысл», когда менеджер обосновывает его последовательными доказательствами, основанными на ранее накопленном опыте;
•методы, основанные на научно-практическом подходе, предполагающем выбор оптимальных решений, с применением современных технических средств, на основе переработки больших объемов информации, помогающих обосновывать принимаемые решения.
В этой связи была предложена авторская классификация научно-практических методов ПУР по признаку применения в прикладных областях менеджмента (табл.1) [3].
Таблица 1
Классификация методов ПУР по направлениям использования в прикладном менеджменте
|
№ |
Направления развития менеджмента |
Состав классов методов ПУР |
|
1 |
Общий менеджмент |
1.1.Общенаучные методы [1, c. 254–256]. 1.2. Методы, основанные на традиционных способах обработки информации и принятия решений[1, c. 257–270]. 1.3. Методы на основе детерминированного факторного анализа [1, c. 271–282]. 1.4. Методы на основе стохастического факторного анализа [1, c. 283–298]. |
|
2 |
Менеджмент организации |
2.1. Методы, основанные на комплексном экономическом анализе хозяйственной деятельности (АХД) организации [1, c. 436–443]; 2.2. Методы, основанные на оценке перспектив развития производственно-хозяйственной деятельности экономических систем (предприятий), с учетом их инновационного потенциала и инвестиционных возможностей [1, c. 479–503]; 2.3. Методы на основе технологий организационного управления [4, c. 133–135]. |
|
3 |
Исследование систем управления |
3.1. Методы оптимизации показателей эффективности на основе линейного программирования [1, c. 299–301]; 3.2. Методы оптимизации показателей эффективности на основе нелинейного программирования 3.3. Методы оптимизации показателей эффективности на основе динамического программирования. |
|
4 |
Стратегический менеджмент |
4.1. Методы, базирующиеся на основе анализа схем стратегического развития экономических систем [1, c. 308–330]; 4.2. Методы выбора стратегий развития экономических систем с позиций оценки их рыночной конкурентоспособности [5, c. 153]. |
|
5 |
Антикризисное управление |
5.1. Методы антикризисного управления на основе технологий А-моделей оценки; 5.2. Методы антикризисного управления на основе технологий Z-моделей оценки [6, c. 329–345]. |
|
6 |
Логистика |
6.1. Методы закупочной логистики [7, c. 164–207]; 6.2. Методы производственной логистики [7, c. 215–271]; 6.3. Методы распределительной логистики[7, c. 273–278];
|
|
7 |
Управление персоналом |
7.1. Методы, связанные с управлением персоналом [1, c. 331–338]. |
|
8 |
Инновационный менеджмент |
8.1.Методы на основе технологий поиска инновационных путей развития [1, c. 412–429]; 8.2. Методы на основе бизнес-моделей новаторов бизнеса [1, c. 430–435]; 8.3. Методы, основанные на технологиях управления инновационными проектами [8, c. 97–107]. |
|
9 |
Информационные технологии управления |
9.1. Методы выявления альтернатив для принятия управленческого решения по технологиям OLAP и Data Mining [3]; 9.2. Методы интеллектуального анализа данных [3]; 9.3. Методы оценки альтернатив – сценарного моделирования «что-если» [3]. |
|
10 |
Управление качеством |
10.1. Методы, основанные на инструментах управления качеством [1, c. 339–372]; 10.2. Методы на основе теории квалиметрии [9, c. 275–306]. |
|
11 |
Финансовый менеджмент |
11.1. Методы, основанные на комплексном экономическом анализе хозяйственной деятельности (АХД) организации [1, c. 436–443]; 11.2. Методы, основанные на оценке активов и капитала экономических систем) [1, c. 465–473]; 11.3. Методы, связанные с управлением структурой капитала экономических систем (предприятий) [1, c. 465–473]. |
|
12 |
Инвестиционный менеджмент |
12.1. Методы инвестиционного характера, основанные на оценке стоимости капитала экономических систем (предприятий) [10, c. 170–171] |
|
13 |
Управление проектами |
13.1. Методы, основанные на принципах классического проектного управления [11, c. 44–61]; 13.2. Методы, основанные на технологиях управления инновационными проектами [8, c. 97–107] |
|
14 |
Риск-менеджмент |
14.1. Методы оценки риска, основанные на теории игр[1, c. 303–307, с. 518–525]; 14.2. Статистические методы оценки рисков [1, c. 526–542]; 14.3. Методы анализа и оценки портфельных рисков инвестирования [1, c. 542–569]; 14.4. Методы оценки рисков на основе теории массового обслуживания [1, c. 301–303]; 14.5. Методы оценки рисков абсолютной величины вероятных потерь инвестиций [12, с. 34]; 14.6. Специализированные методы оценки рисков инвестиционных проектов [12, с. 35]. |
|
15 |
Производственный менеджмент
|
15.1. Организационные методы [3]. 15.2. Административные методы [3]. 15.3. Экономические методы [3]. 15.4. Социально-психологические методы [3]. |
|
16 |
Экологический менеджмент |
16.1. Административные методы [13]. 16.2. Методы экологической экспертизы [13]. 16.3. Экономические методы [13]. 16.4. Социально-психологические методы [13]. |
|
17 |
Тайм-менеджмент |
17.1. Методы управления в тайм-менеджменте при целеполагании [3]. 17.2. Методы управления персональным временем [3]. 17.3. Методы планирования в тайм-менеджменте [3]. 17.4. Методы повышения скорости работы [3]. |
В проведенных ранее исследованиях были рассмотрены:
– общенаучные методы ПУР, включая [3]: метод восхождения от абстрактного к конкретному; методы анализа и синтеза; методы индукции и дедукции; метод единства логического и исторического; метод системного анализа; метод комплексного анализа; методы дифференциации и интеграции; метод программно-целевого планирования; экономические методы; административные методы; социально-психологические методы:
– методы ПУР, основанные на традиционных способах обработки информации принятия решений, включая [14]: методы сравнения относительных и средних величин; графические методы; методы группировки; балансовый метод.
В данной работе рассматриваются методы ПУР на основе детерминированного факторного анализа, включая [1, c. 271–282]: метод цепных подстановок; индексный метод; метода абсолютных разниц; метода относительных разниц; интегральный метод; метод простого прибавления неразложимого остатка; логарифмический метод; метод пропорционального деления (долевого участия); метод дифференциального исчисления; методом взвешенных конечных разностей; метод коэффициентов; методом дробления приращения факторов.
Дадим общую характеристику методов ПУР на основе детерминированного факторного анализа.
Принятие управленческих решений на основе детерминированного факторного анализа базируется на использовании точной функциональной связи между воздействующими факторами хi и результирующим показателем y. Наиболее часто детерминированный факторный анализ связан с использованием моделей следующих типов:
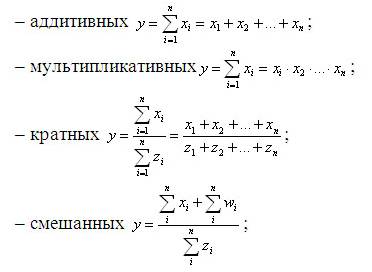
и т.д.
При принятии управленческих решений на основе методов детерминированного факторного анализа одним из ключевых вопросов является определение величины влияния отдельных факторов на прирост результирующих показателей, для чего используются способы: цепных подстановок, индексный, абсолютных разниц, относительных разниц, пропорционального деления, интегральный, логарифмирования и др.
В основе использования этих методов лежит принцип элиминирования – исключения («замораживания») воздействия всех факторов на величину результативного показателя, кроме одного. При этом считается, что все воздействующие на результат факторы независимы.
Рассмотрим основные методы детерминированного факторного анализа, используемые при принятии управленческих решений.
Метод цепных подстановок заключается в определении ряда промежуточных значений результативного показателя y путем последовательной замены базисной величины каждого воздействующего факторного a0,b0,c0,d0 на отчетную a1,b1,c1,d1. В результате чего обеспечивается выделение влияния каждого фактора. Например, связь между результативным показателем y и воздействующими факторами a,b,c,d определяется мультипликативной моделью [1, c. 272]:
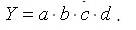
Тогда, базисное значение Y0 рассчитывается по формуле:
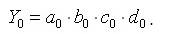
Отчетное значение результативного показателя Y1 определяется выражением:

Условные значения результативного показателя yа, yв, yс, yd рассчитываются соответственно из выражений:
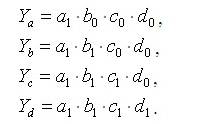
Тогда влияние каждого фактора на результат можно описать в виде:
∆Yа= Yа-Y0
∆Yb= Yb-Yа
∆Yc= Yc-Yb
∆Yd= Yd-Yc.
В силу своей простоты, универсальности и наглядности метода цепных подстановок часто используются при принятии управленческих решений на основе результатов детерминированного факторного анализа.
Индексный способ обработки информации при принятии решений основан на вычислении относительных показателей динамики, пространственных сравнений, выполнения плана (норматива, прогноза) и т.д. [1, c. 273–275].
Основной формой индекса является агрегатный (от латинского agregatus – складываемый, суммируемый), в котором числитель и знаменатель представляют собой набор («агрегат») непосредственно несоизмеримых и неподдающихся суммированию элементов – сумму произведений двух величин, одна из которых меняется (индексируется), а другая остается неизменной (вес индекса).
Примером общего индекса количественных показателей может служить агрегатный индекс стоимости продукции или товарооборота:
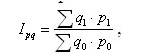
где ∑q1p1 – стоимость продукции отчетного периода,
∑q0p0 – стоимость продукции базисного периода,
p1, p0 – цены единицы продукции в отчетном и базисном периоде соответственно (p – от латинского pretium),
q1, q0 – количество какой-либо продукции в натуральном выражении в отчетном и базисном периоде соответственно (q – от латинского quantitas).
Индекс Ipq показывает во сколько раз изменилась стоимость продукции отчетного периода по сравнению с базисным.
Агрегатный индекс физического объема продукции Iq отражает изменение только одного фактора – индексируемого показателя объема продукции q, реализуемой по одним и тем же ценам, например, базисным p0:
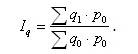
Этот же общий индекс физического объема Iq можно представить в форме среднего арифметического индекса:
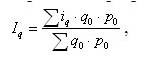
где iq=q1:q0 – индивидуальный индекс объема продукции.
Такой индекс используется, например, когда неизвестны количества произведенных отдельных видов продукции в натуральных измерениях, но известны индивидуальные индексы iq и общая стоимость продукции базисного периода q0p0.
В аналитических целях может быть также использован общий индекс физического объема Iq, представленный в форме среднего гармонического индекса:
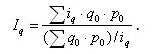
Рассмотренные выше общие индексы рассчитываются для количественных показателей. Наряду с ними широкое распространение получили общие индексы качественных показателей.
Характерными примерами общих индексов качественных показателей являются агрегатные индексы цен.
Агрегатный индекс с весами объема продукции по отчетному периоду, предложенный в 1874 г. немецким экономистом Г. Пааше, вычисляют по формуле:
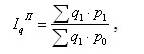
где ∑q1p1 – фактическая стоимость товаров в отчетном периоде,
∑q1p0 – условная стоимость товаров, реализованных в отчетном периоде по ценам базисного периода.
Агрегатный индекс с весами объема продукции по базисному периоду, предложенный в 1864 г. немецким экономистом Э.Ласпейресом, вычисляют по формуле:
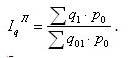
Значения индексов цен Пааше и Ласпейреса для одних и тех же данных не совпадают, так как имеют различное экономическое содержание. Индекс цен Пааше характеризует изменение цен отчетного периода по сравнению с базисным по товарам, реализованным в отчетном периоде и фактическую экономию (или перерасход) от изменения цен. Индекс цен Ласпейреса характеризует изменение цен отчетного периода по сравнению с базисным по товарам, реализованным в базисном периоде и экономию (или перерасход), которую можно было бы получить от изменения цен (то есть условную экономию).
Частичное устранение недостатков, присущих индексам Ласпейреса и Пааше, при расчете индекса инфляции обеспечивает индекс Фишера (IF), суть которой заключается в вычислении среднего геометрического значения индексов Ласпейреса (IL) и Пааше (IP):
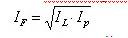
В силу своей универсальности и наглядности индексный метод широко используется при принятии управленческих решений в макроэкономике на основе результатов детерминированного факторного анализа.
Метод абсолютных разниц используется в мультипликативных и мультипликативно-аддитивных моделях и заключается в расчете величины влияния факторов умножением абсолютного прироста исследуемого фактора на базовую величину фактора, находящегося справа от него и на фактическую величину факторов, расположенных слева. Например, для мультипликативной факторной модели типа изменение величины влияния каждого фактора на результативный показатель определяется из выражений [1, c. 275]:
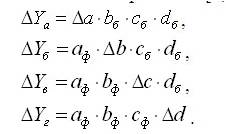
где aб,bб,cб,dб – значения показателей в базисном периоде,
aф,bф,cф,dф – значения показателей в отчетном периоде,
∆a=аф-аб, ∆b=bф-bб, ∆c=сф-сб, ∆d=dф-dб.
Метод абсолютных разниц позволяет оценить при принятии управленческих решений абсолютное влияние на изменение результата вариации каждого из факторов.
Метод относительных разниц, как и способ абсолютных разниц, используется лишь в мультипликативных и мультипликативно-аддитивных моделях для измерения влияния факторов на прирост результативного показателя. Он заключается в расчете относительных отклонений величин факторных показателей с последующим расчетом изменения результативного показателя Yф за счет каждого фактора относительно базового Yб. Например, для мультипликативной факторной модели типа изменение величины влияния каждого фактора на результативный показатель определяется следующим образом [1, c. 275]:
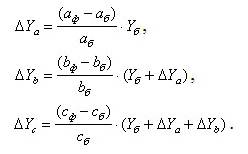
Метод относительных разниц, обладая высоким уровнем наглядности, обеспечивает получение тех же результатов, что и метод абсолютных разниц при меньшем объеме вычислений, что достаточно удобно при принятии управленческих решений на основе моделей детерминированного факторного анализа с большим числом факторов.
Метод пропорционального деления (долевого участия) используется для аддитивных Y=a+b+c и кратных моделей типа Y=a/(b+c+d), в том числе многоуровневых. Этот метод заключается в пропорциональном распределении прироста результативного показателя Y за счет изменения каждого из факторов между ними. Например, для аддитивной модели типа Y=a+b+c влияние факторов рассчитывается [1, c. 276]:
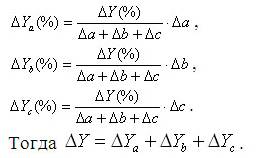
Если считать, например, что Y – себестоимость продукции; a, b, c – составляющие себестоимости – затраты на материалы, оплату труда и амортизацию соответственно, то можно используя метод пропорционального деления оценить степень влияния каждого из факторов. Если уровень общей рентабельности предприятия снизился на 10% в связи с увеличением себестоимости продукции на 200 тыс. руб, а при этом затраты на материалы сократились на 60 тыс. руб., затраты на оплату труда выросли на 250 тыс. руб., а затраты на амортизацию выросли на 10 тыс. руб., то можно показать, что за счет первого фактора (а) – затрат на материалы уровень рентабельности вырос на:
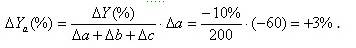
За счет второго (b) – затраты на оплату труда и третьего (с) – затраты на амортизацию факторов уровень рентабельности снизился на:

Метод пропорционального деления (долевого участия) удобен при принятии управленческих решений на основе моделей детерминированного факторного анализа, связанных с распределением ресурсов и результатов деятельности.
Метод дифференциального исчисления предполагает, что общее приращение функции различается на слагаемые, где значение каждого из них определяется как произведение соответствующей частной производной на приращение переменной, по которой вычислена данная производная [1, c. 277].
Рассмотрим функцию 2-х переменных: z=f(x,y). Если эта функция дифференцируема, то ее приращение можно представить:

где ∆z=(z1-z0) – изменение функции;
∆x=(х1-х0) – изменение первого фактора;
∆y=(y1-y0) – изменение второго фактора;
– величина неразложимого остатка.
Сумма – главная часть приращения дифференцируемой функции, (которая и учитывается в методе дифференциального исчисления).
– неразложимый остаток, являющийся бесконечно малой величиной при достаточно малых изменениях факторов х и у. Эта составляющая не учитывается в рассматриваемом методе дифференциального исчисления. Однако при существенных изменениях факторов (∆xи ∆y) могут возникнуть значительные ошибки в оценке влияния факторов.
Рассмотрим пример. Функция z имеет вид z=x*y, для которой известны начальные и конечные значения воздействующих факторов и результирующего показателя (x0,y0,z0,x1,y1,z1). Тогда влияние воздействующих факторов на величину результирующего показателя определяется выражениями:
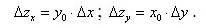
Вычисление величины остаточного члена как разницы между величиной общего изменения функции
 и суммой влияний
и суммой влияний
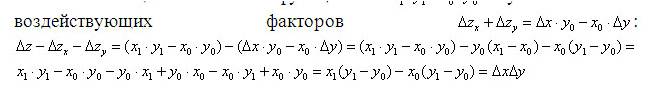
Таким образом, в методе дифференциального исчисления неразложимый остаток просто отбрасывается (логическая ошибка метода дифференцирования). Эта приближенность рассмотренного метода является недостатком для экономических расчетов, где требуется точный баланс изменения результирующего показателя и суммы влияния воздействующих факторов.
По указанной причине метод дифференциального исчисления имеет ограниченное применение при принятии управленческих решений на основе моделей детерминированного факторного анализа.
Метод простого прибавления неразложимого остатка подразумевает равномерное распределение этого остатка между факторами [1, c. 278]. Например, для рассмотренной выше функции z вида влияние приращения факторов можно представить в виде:
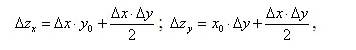
либо в другом варианте
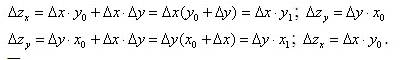
Преимуществом данного метода является решение проблемы остаточного члена. Недостатком метода простого прибавления неразложимого остатка является то, что результат разложения общего прироста результирующего показателя, осуществляемый методом цепных подстановок, зависит от порядка подстановки. В связи с этим затрудняется получение однозначного количественного значения влияния отдельных факторов, что несколько ограничивает использование метода простого прибавления неразложимого остатка при принятии управленческих решений на основе моделей детерминированного факторного анализа.
Метод взвешенных конечных разностей предполагает, что величина влияния каждого фактора определяется по каждому из вариантов подстановки факторов, после чего результаты суммируются и от полученной суммы берется средняя величина, дающая единый ответ о значении влияния фактора [1, c. 278]. Так для функции z вида влияние приращения факторов определяется следующим образом:
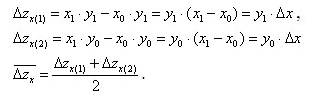
Аналогично
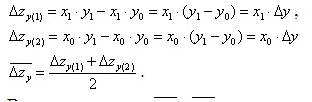
В результате
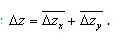
Учет влияния каждого фактора как усредненного значения по каждому из вариантов подстановки факторов обеспечивает достаточно активное использование метода взвешенных конечных разностей при принятии управленческих решений.
Логарифмический метод детерминированного факторного анализа заключается в логарифмически пропорциональном распределении остатка по искомым факторам и применяется в мультипликативных моделях. Результаты расчетов не зависят от местоположения факторов в модели [1, c. 279].
Например, для функции f вида f=x∙y∙z
lg(f)=lg(x)+lg(y)+lg(z).
Поскольку между индексами использования показателей используются та же зависимость, что и между самими показателями, произведя замену абсолютных значений на индексы, имеем:
lg(f1/f0)=lg(x1/x0)+lg(y1/y0)+lg(z1/z0)
или
lg(If)=lg(Ix)+lg(Iy)+lg(Iz).
Разделив обе части равенства на lg(If) и умножив на ∆f получим:
∆f=∆f∙lg(Ix)/lg(If)+∆f∙lg(Iy)/lg(If)+∆f∙lg(Iz)/lg(If).
Влияние отдельных факторов определяется следующим образом:
∆fх=lg(Ix)/lg(If); ∆fу=lg(Iy)/lg(If); ∆fz=lg(Iz)/lg(If).
Таким образом, результативный показатель распределяется по факторам пропорционально отношениям логарифмов факторных индексов к логарифму индекса результативного показателя.
Достоинством логарифмического метода является высокая точность (более высокая, чем при интегральном способе), а также распределение совместного действия факторов пропорционально доле изолированного влияния каждого фактора на уровень результативного показателя. Недостаток логарифмического метода заключается в ограниченной сфере его применения. Поэтому при принятии управленческих решений на основе моделей детерминированного факторного анализа логарифмический метод используется достаточно редко.
Метод коэффициентов основан на сопоставлении числовых значений одних и тех же базисных экономических показателей при разных условиях [1, c. 279]:
∆z=z1-z0=y1/x1-y0/x0=∆zx+∆zy,
∆zx=z0∙Kx=z0∙(x1-x0)/x0= z0∙∆x/x0,
∆zy=z0∙Ky=z0∙(y0-y1)/y0= z0∙∆y/y0.
Достоинство метода заключается в его относительной простоте. Недостаток – результат суммарного влияния факторов не совпадает с величиной изменения результативного показателя, подсчитанной прямым способом.
Несмотря на свой недостаток метод коэффициентов позволяет при принятии управленческих решений оценить различные варианты решений на основе сопоставления числовых значений одних и тех же базисных экономических показателей при разных условиях моделей.
Интегральный метод детерминированного факторного анализа применяется для определения влияния факторов в мультипликативных, кратных и смешанных моделях кратно-аддитивного вида, позволяя получить более точные результаты вычисления влияния факторов по сравнению со способами цепной подстановки, абсолютных и относительных разниц и избежать неоднозначной оценки влияния [1, c. 280–281]. Дело в том, что при использовании интегрального метода результаты не зависят от местоположения факторов в модели, а дополнительный прирост результативного показателя, возникающий из-за взаимодействия факторов, распределяется между ними поровну.
Таким образом, интегральный метод детерминированого факторного анализа позволяет нейтрализовать недостаток, присущий способу элиминирования, при котором предполагается, что факторы, определяющие результат, изменяются независимо друг от друга. На самом деле в подавляющем большинстве случаев воздействующие факторы взаимосвязаны в своем влиянии на результат. Учет этого совместного влияния факторов при элиминировании производится с использованием неразложимого остатка, прибавляемого, как правило, к величине влияния последнего фактора, представленного в модели факторного анализа. То есть величина влияния каждого фактора на изменение результативного показателя изменяется в зависимости от места расположения фактора в детерминированной модели. Именно этот недостаток и исключает интегральный метод.
Вычисление влияния факторов с помощью интегрального метода является более точным по сравнению с методами цепных подстановок, абсолютных и относительных разниц, поскольку результаты не зависят от местоположения факторов в модели, а дополнительный прирост результативного показателя, возникающий вследствие взаимодействия факторов (синергетический эффект), распределяется между рассматриваемыми факторами поровну.
Для мультипликативной двухфакторной модели F=x∙y влияние факторов описывается следующим образом:
∆Fx=∆x∙y0+(∆x∙∆y)/2,
∆Fy=∆y∙x0+(∆x∙∆y)/2.
Для мультипликативной трехфакторной модели F=x∙y∙z влияние факторов описывается:
∆Fx=∆x∙(y0∙z1+y1∙z0)/2+(∆x∙∆y∙∆z)/3,
∆Fy=∆y∙(x0∙z1+x1∙z0)/2+(∆x∙∆y∙∆z)/3,
∆Fz=∆z∙(x0∙y1+x1∙y0)/2+(∆x∙∆y∙∆z)/3.
Для мультипликативной четырехфакторной модели F=x∙y∙z∙g влияние факторов определяется:
∆Fx=∆x∙{3∙y0∙z0∙g0+y1∙g0∙(z1+∆z)+g1∙z0∙(y1+∆y)+z1∙y0∙(g1+∆g)}/6+(∆x∙∆y∙∆z∙∆g)/4 и т.д.
Для кратной модели вида влияние факторов описывается следующим образом:
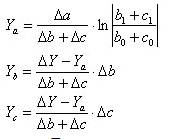
Благодаря своим достоинствам интегральный метод активно используется при принятии управленческих решений на основе моделей детерминированного факторного анализа.
Области применения основных методов детерминированного факторного анализа, используемых при принятии управленческих решений, приведены в табл.1.
Таблица 1
Области применения основных методов детерминированного факторного анализа, используемых при принятии управленческих решений
|
Модели Метод |
Мультипли- кативные |
Аддитив- ные |
Кратные |
Смешанные |
|
Цепных подстановок |
+ |
+ |
+ |
+ |
|
Индексный |
+ |
- |
+ |
- |
|
Абсолютных разниц |
+ |
- |
- |
+ |
|
Относительных разниц |
+ |
- |
- |
- |
|
Пропорционального деления (долевого участия) |
- |
+ |
- |
+ |
|
Интегральный |
+ |
- |
+ |
+ |
|
Логарифмический |
+ |
- |
- |
- |
Достоинства и недостатки методов детерминированного факторного анализа, используемых при принятии управленческих решений, приведены в табл. 2.
Таблица 2
Достоинства и недостатки методов детерминированного факторного анализа, используемых при принятии управленческих решений
|
Метод |
Достоинства |
Недостатки |
|
Цепных подстановок |
Универсальность, наглядность |
Зависимость результата оценки от порядка подстановки факторов |
|
Индексный |
Относительность общей безразмерной оценки, наглядность |
Погрешность, вносимая условными оценками на фоне фактических |
|
Абсолютных разниц |
Обеспечение абсолютной оценки влияния фактора на результат, наглядность |
Зависимость результата оценки от порядка подстановки факторов |
|
Относительных разниц |
Обеспечение относительной оценки влияния фактора на результат, наглядность, сокращение объема вычислений по сравнению с методом абсолютных разниц |
Зависимость результата оценки от порядка подстановки факторов |
|
Пропорционального деления (долевого участия) |
Обеспечение пропорционального распределения прироста результативного показателя от влияния факторов |
Зависимость результата оценки от порядка подстановки факторов |
|
Дифференциального исчисления |
Универсальность |
Неразложимый остаток просто отбрасывается, что увеличивает погрешность метода |
|
Простого прибавления неразложимого остатка |
Относительно метода дифференциального исчисления метод простого прибавления неразложимого остатка решает проблему остаточного члена |
Зависимость результата оценки от порядка подстановки факторов |
|
Взвешенных конечных разностей |
Влияние каждого фактора определяется как усредненное по каждому из вариантов подстановки факторов |
Относительно большой объем вычислений |
|
Логарифмический |
Относительно высокая точность и распределение совместного влияния факторов пропорционально доле изолированного их влияния на уровень результативного показателя |
Ограниченность области применения (только для мультипликативных моделей) |
|
Коэффициентов |
Относительно прост |
Погрешности в оценке – результат суммарного влияния факторов не совпадает с величиной изменения результативного показателя |
|
Интегральный |
Исключает недостатки, присущие тем методам, где считается, что факторы, определяющие результат, изменяются независимо друг от друга. То есть учитывает синергетический эффект совместного влияния факторов на результат. Является достаточно точным, поскольку результат оценки не зависит от местоположения факторов в модели |
Относительно большой объем вычислений |
Таким образом, принятие управленческих решений на основе детерминированного факторного анализа наиболее эффективно при работе с мультипликативными моделями. Аддитивные модели при этом напротив – сопряжены с наибольшей сложностью при обработке.
Самым универсальным методом детерминированного факторного анализа, обеспечивающим принятие решения, является метод цепных подстановок. А метод относительных разниц и логарифмический метод – напротив, самыми узкопрофильными, применимыми лишь для мультипликативных моделей.
Наиболее точным является интегральный метод.
1. Тебекин А.В. Методы принятия управленческих решений. - М.: Юрайт, 2016.
2. Тебекин А.В., Тебекина А.А. Классификация методов принятия управленческих решений. // Журнал исследований по управлению. Volume 2, issue 11. Дата выхода номера: 01 Декабря 2016.
3. Тебекин А.В., Тебекин П.А.Содержание общенаучных методов принятия управленческих решений в менеджменте. // Журнал исследований по управлению. Volume 3, issue 1. Дата выхода номера: 25 Января 2017.
4. Тебекин А.В., Тебекин П.А., Тебекина А.А. Использование информационно-технологической модели управления (ИТМУ) в принятии решений. // Вестник Московского университета им. С.Ю. Витте. Серия 1: Экономика и управление. - 2016. - № 1 (16). - С. 128-135.
5. Тебекин А.В. Теория управления. - М.: Кнорус, 2017. - 342с.
6. Тебекин А.В., Анисимов В.Г., Анисимов Е.Г., Петров В.С., Родионова Е.С., Сауренко Т.Н., Тебекин П.А.Теоретические основы управления инновациями. Научная монография. Под ред. проф. Тебекина А.В. - СПб.: Стратегия будущего, 2016. - 474с.
7. Тебекин А.В. Логистика: учебник. Издание 2-е. - М.: Дашков и К, 2014. - 356 с.
8. Тебекин А.В., Тебекин П.А. Прединвестиционная фаза проектного цикла по модели UNIDO как элемент методической базы разработки и реализации инновационных проектов и программ. // Вестник Московского университета им. С.Ю. Витте. Серия 1: Экономика и управление. -2016. -№ 3 (18). - С. 97-107.
9. Тебекин А.В. Управление качеством. - М.: Юрайт, 2013. - 384 с.
10. Тебекин А.В., Мантусов В.Б. Управление организацией: теоретико-методологические основы, функциональные задачи, технологии, прикладные аспекты применения. Монография. - Москва, 2016.
11. Тебекин А.В., Широкова Л.Н., Сурат И.Л. Управление инновационными проектами. Монография. - М.: Риалтекс, 2014. - 126с.
12. Тебекин А.В. Технологии экономического и таможенного риск-менеджмента как инструменты развития Евразийского экономического союза. В сборнике: Основные проблемы развития таможенного дела России в условиях ее членства в экономических интеграционных объединениях Сборник материалов Международной научно-практической конференции. Федеральная таможенная служба, ГКО ВПО "Российская таможенная академия". - 2015. - С. 31-37.
13. Тебекин А.В. Теоретические основы управления инновационной деятельностью. Монография. Русайнс, 2016. - 213с.
14. Тебекин А.В., Тебекин П.А., Тебекина А.А. Методы принятия управленческих решений на основе традиционных способов анализа и обработки информации. // Журнал исследований по управлению. Volume 3, issue2, 14.03.2017.








