Московский государственный университет им. М.В. Ломоносова (кафедра социокультурного проектирования и развития территорий, профессор)
Москва, г. Москва и Московская область, Россия
Тюмень, Тюменская область, Россия
Россия
Рассмотрены методы принятия управленческих решений на основе стохастического факторного анализа. Представлены результаты разработки алгоритма принятия решения с использованием системы методов стохастического факторного анализа. Показано, что в сочетании с общенаучными методами, методами, основанными на традиционных способах обработки информации и принятия решений, методами на основе детерминированного факторного анализа, методы на основе стохастического факторного анализа образуют полную систему принятия решений в общем менеджменте. Представлено, что схема взаимосвязи методов принятия решений в системе общего менеджмента является: самодостаточной, инвариантной к специфике менеджмента организации и соответствует инжиниринговому подходу.
стохастический факторный анализ, принятие управленческих решений.
В процессе ускорения научно-технического прогресса неизменно усложняются создаваемые человеком социально-экономические системы и решаемые ими задачи, что требует адекватного развития инструментов и методов принятия управленческих решений (ПУР) [1].
Чем глубже человек проникает в сущность изучаемых явлений, тем более точные методы исследования ему требуются и тем более рациональные варианты решений он получает [2, с. 245–246].
Поскольку известные классификации научно-практических методов принятия решений [3–7] не дают возможность признать их исчерпывающими, Тебекиным А.В. была предложена классификация научно-практических методов ПУР по признаку применения в прикладных областях менеджмента [1] в результате обобщения выполненных ранее исследований [1], [8–15], [22–31], и был определен состав групп методов ПУР для каждого из классов (табл. 1) [32].
Результаты формирования системы классификации научно-практических методов ПУР по признаку применения в прикладных областях менеджмента, построенной на базе классификации [8, с. 61–62], и являющаяся результатом обобщения выполненных ранее исследований [1], [8–15], [22–31] (табл. 1) [32].
Таблица 1
Классификация методов ПУР по направлениям использования в прикладном менеджменте
|
№ |
Направления развития менеджмента |
Состав классов методов ПУР |
|
1 |
Общий менеджмент |
Универсальные методы ПУР: 1.1.Общенаучные методы [2, c. 254–256]. 1.2. Методы, основанные на традиционных способах обработки информации и принятия решений [2, c. 257–270]. 1.3. Методы на основе детерминированного факторного анализа [2, c. 271–282]. 1.4. Методы на основе стохастического факторного анализа [2, c. 283–298] |
|
2 |
Менеджмент организации |
2.1. Методы, основанные на комплексном экономическом анализе хозяйственной деятельности (АХД) организации [2, c. 436–443]. 2.2. Методы, основанные на оценке перспектив развития производственно-хозяйственной деятельности экономических систем (предприятий), с учетом их инновационного потенциала и инвестиционных возможностей [2, c. 479–503]. 2.3. Методы на основе технологий организационного управления [15, c. 133–135] |
|
3 |
Исследование систем управления |
3.1. Методы оптимизации показателей эффективности на основе линейного программирования [2, c. 299–301]. 3.2. Методы оптимизации показателей эффективности на основе нелинейного программирования. 3.3. Методы оптимизации показателей эффективности на основе динамического программирования |
|
4 |
Стратегический менеджмент |
4.1. Методы, базирующиеся на основе анализа схем стратегического развития экономических систем [2, c. 308–330]. 4.2. Методы выбора стратегий развития экономических систем с позиций оценки их рыночной конкурентоспособности [14, c. 153] |
|
5 |
Антикризисное управление |
5.1. Методы антикризисного управления на основе технологий А-моделей оценки. 5.2. Методы антикризисного управления на основе технологий Z-моделей оценки [25, c. 329–345] |
|
6 |
Логистика |
6.1. Методы закупочной логистики [16, c. 164–207]. 6.2. Методы производственной логистики [16, c. 215–271]. 6.3. Методы распределительной логистики [16, c. 273–278].
|
|
7 |
Управление персоналом |
7.1. Методы, связанные с управлением персоналом [2, c. 331–338] |
|
8 |
Инновационный менеджмент |
8.1. Методы на основе технологий поиска инновационных путей развития [2, c. 412–429]. 8.2. Методы на основе бизнес-моделей новаторов бизнеса [2, c. 430–435]. 8.3. Методы, основанные на технологиях управления инновационными проектами [17, c. 97–107] |
|
9 |
Информационные технологии управления |
9.1. Методы выявления альтернатив для принятия управленческого решения по технологиям OLAP и Data Mining [1]. 9.2. Методы интеллектуального анализа данных [1]. 9.3. Методы оценки альтернатив – сценарного моделирования «что-если» [1] |
|
10 |
Управление качеством |
10.1. Методы, основанные на инструментах управления качеством [2, c. 339–372]. 10.2. Методы на основе теории квалиметрии [17, c. 275–306] |
|
11 |
Финансовый менеджмент |
11.1. Методы, основанные на комплексном экономическом анализе хозяйственной деятельности (АХД) организации [2, c. 436–443]. 11.2. Методы, основанные на оценке активов и капитала экономических систем [2, c. 443–465]. 11.3. Методы, связанные с управлением структурой капитала экономических систем (предприятий) [2, c. 465–473] |
|
12 |
Инвестиционный менеджмент |
12.1. Методы инвестиционного характера, основанные на оценке стоимости капитала экономических систем (предприятий) [18, c. 170–171]. |
|
13 |
Управление проектами |
13.1. Методы, основанные на принципах классического проектного управления [19, c. 44–61]. 13.2. Методы, основанные на технологиях управления инновационными проектами [29, c. 97–107] |
|
14 |
Риск-менеджмент |
14.1. Методы оценки риска, основанные на теории игр [2, c. 303–307, с. 518–525]. 14.2. Статистические методы оценки рисков [2, c. 526–542]. 14.3. Методы анализа и оценки портфельных рисков инвестирования [2, c. 542–569]. 14.4. Методы оценки рисков на основе теории массового обслуживания [2, c. 301–303]. 14.5. Методы оценки рисков абсолютной величины вероятных потерь инвестиций [20, с. 34]. 14.6. Специализированные методы оценки рисков инвестиционных проектов [20, с. 35] |
|
15 |
Производственный менеджмент
|
15.1. Организационные методы [1]. 15.2. Административные методы [1]. 15.3. Экономические методы [1]. 15.4. Социально-психологические методы [1] |
|
16 |
Экологический менеджмент |
16.1. Административные методы [13]. 16.2. Методы экологической экспертизы [13]. 16.3. Экономические методы [13]. 16.4. Социально-психологические методы [13] |
|
17 |
Тайм-менеджмент |
17.1. Методы управления в тайм-менеджменте при целеполагании [1]. 17.2. Методы управления персональным временем [1]. 17.3. Методы планирования в тайм-менеджменте [1]. 17.4. Методы повышения скорости работы [1] |
|
18 |
GR- менеджмент |
18.1. Методы обеспечения партнерских отношений с государственными органами [21]. 18.2. Методы обеспечения благоприятного административного климата для организации [21]. 18.3. Методы недопущения принятия государственными органами нормативно- правовых актов, ухудшающих положение организации [21]. 18.4. Методы обеспечения участия организации в реализации государственных программ, получения государственной поддержки и экономического сотрудничества с государством [21]. 18.5. Методы поддержки принятия законодательных актов, способствующих развитию организации и т.д. [21] |
Очевидно, что при разработке и принятии управленческих решений не идет речь о совместном использовании всех классов методов, представленных в табл. 1.
В то же время представляется целесообразным рассмотрение вопроса о совместном использовании различных классов методов принятия управленческих решений, представленных в табл. 1, способных рационально дополнить друг друга.
Этому вопросу и посвящено приводимое ниже рассмотрение.
Центральное место среди классов методов ПУР, представленных в табл. 1 занимают методы общего менеджмента (блок 1 табл. 1), именуемые также универсальными.
Характеристики общенаучных методов принятия управленческих решений, состав которых представлен в табл. 2 [32], и используемых в общем менеджменте в качестве методологической базы обоснования управленческих решений, подробно рассмотрены в работе [1].
Таблица 2
Общенаучные методы принятия управленческих решений, используемые в общем менеджменте
|
№ |
Состав МПУР |
Характеристика МПУР |
|
1 |
Метод восхождения от абстрактного к конкретному |
Способ изучения действительности, предполагающий последовательный переход от абстрактных и односторонних представлений о ней ко всё более конкретному её воспроизведению в теоретическом мышлении и практике, что и способствуют принятию обоснованных управленческих решений |
|
2 |
Методы анализа и синтеза |
Как методы научного познания предполагают реальное или мысленное разложение исследуемого объекта управления на компоненты с целью последующего мысленного объединения этих компонентов в различных вариантах в целостный объект и выбора наилучшего варианта реального объединения рассматриваемых компонентов в целостный объект в интересах эффективного управления |
|
3 |
Методы индукции и дедукции |
Методы индукции представляют собой технологию установления причинных связей между явлениями, широко используемую при принятии управленческих решений. Метод дедукции представляет собой способ научного исследования, при котором частное положение логическим путём выводится из общего. Для принятия управленческих решений такой способ, основанный на правилах логики особенно актуален, поскольку принятие решения в подавляющем большинстве случаев сопряжено с дефицитом исходной информации и времени на ее обработку (обдумывание). В результате по обобщённым умозаключениям формируется управленческое решение, соответствующее конкретному случаю |
|
4 |
Метод единства логического и исторического
|
Метод основан на принципе развития, включающего в себя процесс становления законов в соответствующей области и направлен на построение модели развивающейся системы, сочетающей исторические и логические аспекты, традиционно сопровождающие обоснование управленческих решений |
|
5 |
Метод системного анализа |
Метод применяется при принятии управленческих решений как способ упорядочения управленческих проблем, благодаря которому осуществляется их структурирование, определяются цели решения, выбираются варианты, устанавливаются взаимосвязи и зависимости элементов проблем, а также факторы и условия, оказывающие воздействие на их решение. При этом метод позволяет за счет реализации последовательности действий установить структурные связи между переменными или элементами исследуемой системы, опираясь на комплекс общенаучных теоретических и экспериментальных, статистических и математических методов и принять научно обоснованное управленческое решение |
|
6 |
Метод комплексного анализа |
Метод предполагает комплексное изучение исследуемого объекта, являясь специфической формой конкретизации системного анализа, так как основу комплексного анализа составляет рассмотрение множества факторов, определяющих характер управления объекта в их связи и взаимозависимости с использованием методов исследований многих наук, изучающих эти же проблемы. Форма междисциплинарной интеграции и кооперации управленческой деятельности, присущая использованию метода комплексного анализа, предопределяет его использование при принятии управленческих решений |
|
7 |
Методы дифференциации и интеграции |
Методы дифференциации и интеграции как общенаучные методы ПУР, тесно связанные с методами дедукции и индукции, оказывают существенное влияние на принятие управленческих решений. При этом метод дифференциации описывает процесс дробления системы на составляющие, а метод интеграции отражает процесс соединения отдельных элементов посредством установления необходимых связей в единую систему, способную эффективно выполнить возлагаемые на нее функции |
|
8 |
Метод программно-целевого планирования |
Метод заключается в ориентации управляемого объекта на достижение поставленных целей посредством отбора основных целей научно-технического, производственно-технологического, социально-экономического или иного развития, разработки комплекса взаимоувязанных мероприятий по достижению этих целей в заданные сроки, предполагающих сбалансированность обеспечения и эффективность использования ресурсов в процессе достижения поставленных целей. Технология реализации метода программно-целевого планирования и управления выстроена по логической схеме «цели управления – пути достижения поставленных целей – способы (инструменты) достижения целей – средства, необходимые для достижения цели» и находит отражение в соответствующей программе принятия и реализации управленческих решений как в комплексном плане реализации необходимых мероприятий |
|
9 |
Экономические методы |
Представляют собой совокупность средств и инструментов целенаправленного воздействия на внутренние переменные предприятия (цели, задачи, технологии, структуру, людей) в интересах создания благоприятных экономических условий хозяйствования, обеспечения эффективного функционирования и развития предприятия в рыночных условиях. При этом экономические методы ПУР опираются на стимулы, призванные обеспечить заинтересованность и ответственность управленческих работников за принимаемые решения и их последствия |
|
10 |
Административные методы |
Административные методы ПУР представляют собой способы осуществления управленческих воздействий на персонал: базирующиеся на власти, дисциплине и взысканиях, на соответствии применяемых методов нормам функционирования органов управления; направленные на реализацию таких мотивов поведения, как осознанная необходимость дисциплины труда, чувство долга и т.п.; отличающиеся прямым характером воздействия (любой административный или регламентирующий акт подлежит обязательному исполнению); обеспечивающие тем самым принятие научно обоснованных управленческих решений |
|
11 |
Социально-психологические методы |
Социально-психологические методы ПУР предполагают применение социальных и психологических механизмов воздействия на отношения работников на предприятии, рассматриваемом как социально-экономическая система, как инструментов косвенного воздействия, учитывающих интересы отдельных индивидов, персонала предприятия в целом, формальных и неформальных отношений между ними |
Характеристики методов принятия управленческих решений, основанных на традиционных способах обработки информации и принятия решений, состав которых представлен в табл. 3 [32], используемых в общем менеджменте в качестве инструментов для предварительной обработки информации при принятии решений, подробно рассмотрены в работе [22].
Таблица 3
Методы принятия управленческих решений, основанные на традиционных способах обработки информации и принятия решений, используемых в общем менеджменте
|
№ |
Состав МПУР |
Характеристика МПУР |
|
1 |
Метод определения относительной величины динамики iд |
Предполагает определение отношения уровня признака в определенный период или момент времени I(t) к уровню этого же признака в предшествующий период или момент времени I(t-1). Относительные величины динамики часто называют темпами роста iд=I(t)/I(t-1) |
|
2 |
Метод определения относительной величины планового задания iпл. |
Предполагает определение отношения уровня, запланированного на предстоящий период Iпл.(t+1), к фактически сложившемуся уровню Iф(t) в этом периоде iпл.з=Iпл.(t+1)/Iф(t).
|
|
3 |
Метод определения относительной величины выполнения планового задания iвып.пл |
Предполагает определение отношения фактически достигнутого в данном периоде уровня I
|
|
4 |
Метод определения относительной величины структуры qс |
Характеризует долю отдельных частей изучаемой совокупности Q
|
|
5 |
Метод определения относительной величины интенсивности |
Характеризует степень распространения или уровень развития того или иного явления в определенной среде:
|
|
6 |
Метод определения относительной величины координации |
Характеризует соотношение отдельных частей целого между собой. При этом за базу может быть принята любая из частей:
|
|
7 |
Метод определения относительной величины сравнения |
Характеризует соотношение одномерных абсолютных величин, характеризующих разные объекты и относящихся к одному и тому же периоду времени:
|
|
8 |
Методы определения степенных средних величин |
Предполагают определение средних величин как обобщающих показателей, характеризующих типичный уровень явления в конкретных условиях места и времени, отражая величину варьирующего признака в расчете на единицу качественно однородной совокупности через среднегармонические, среднеарифметические, среднегеометрические, среднеквадратические и другие степенные значения, удовлетворяющие правилу мажоритарности средних: хгарм ≤ хгеом ≤ харифм ≤ хкв ≤ хкуб. |
|
9 |
Метод определения моды |
Предполагает определение средней величины как наиболее часто встречающегося значения случайной величины, и широко используется при принятии решений на основе изучения покупательского спроса, рыночных цен и т.д. |
|
10 |
Метод определения медианы |
Предполагает определение средней величины, находящейся в середине вариационного ряда и делящей этот ряд на две равные (по числу единиц) части. Медиана находит практическое применение при принятии решений вследствие своего особого свойства – сумма абсолютных отклонений чисел ряда от медианы есть величина наименьшая |
|
11 |
Линейная диаграмма |
Обычно строится в прямоугольной системе координат, в которой на оси абсцисс откладывается воздействующий фактор (зачастую время), а на оси ординат – изучаемый показатель |
|
12 |
Столбиковая диаграмма
|
Строится в прямоугольной системе координат, где каждое значение изучаемого показателя изображается в виде вертикального столбика |
|
13 |
Ленточная (полосовая) диаграмма |
Основания столбиков, отражающие изучаемые объекты, располагаются вертикально, а масштабная шкала, отражающая значения исследуемого показателя – горизонтально |
|
14 |
Круговая секторная диаграмма |
Площадь окружности описывает величину всей изучаемой совокупности, а площади отдельных секторов отображают доли ее составных частей |
|
15 |
Радиальная секторная (лепестковая) диаграмма |
Строится в полярных координатах, где началом отсчета служит центр окружности, а носителями масштабных шкал значений изучаемых показателей – радиус векторы круга |
|
16 |
Фигурные диаграммы |
Подразумевают изображение данных рисунками-символами, наиболее соответствующих существу отображаемых явлений, число и (или) размеры которых определяются их числовыми значениями. |
|
17 |
Метод сетевых графиков |
Предполагает графическое изображение логически взаимосвязанных участков (этапов) работы, согласованных во временном разрезе, и строится в следующей последовательности: – изображение логической последовательности действий (от исхода к итогу); – формирование важнейших данных в рабочие элементы (этапы); – определение сроков начала, продолжительности и времени окончания этапов; – определение критических узлов (нестыковок по срокам взаимозависимых этапов); – развязка критических узлов (согласование по срокам взаимозависимых этапов) |
|
18 |
Метод картограмм (фоновых и точечных) |
Предполагает построение схематической (контурной) карты, на которой отдельные территории в зависимости от величины изображаемого показателя обозначаются с помощью графических символов (штриховки, расцветки, точек) |
|
19 |
Метод картодиаграмм |
Предполагает сочетание в одном изображении контурной карты и диаграммы, когда символы диаграммы (столбики, круги и т.д.) размещаются по всей карте, давая пространственное представление о величинах изучаемых показателей |
|
20 |
Метод типологической группировки |
Решает задачу выявления и характеристики социально-экономических типов путем разделения качественно разнородной совокупности на классы, социально-экономические типы, однородные группы единиц в соответствии с правилами научной группировки. Например, группировки секторов экономики, хозяйствующих субъектов по формам собственности. При топологических группировках выбор группировочных признаков (атрибутивных или количественных) основывается на анализе качественной природы исследуемого явления для выявления существенных признаков |
|
21 |
Метод структурной группировки |
Предполагает – в которой происходит разделение выделенных с помощью типологической группировки типов явлений, однородных совокупностей группы, характеризующие их структуру по какому-либо варьирующему признаку. Например, группировка: хозяйств по объему продукции; депозитов по сроку их привлечения. Анализ структурных группировок, взятых за ряд периодов или моментов времени, показывает изменение структуры изучаемых явлений, т.е. структурные сдвиги. В изменении структуры общественных явлений отражаются важнейшие закономерности их развития |
|
22 |
Метод аналитической (факторной) группировки |
Позволяют исследовать связи и зависимости между изучаемыми явлениями и их признаками. В основе аналитической группировки лежит факторный признак, и каждая выделенная группа характеризуется средними значениями результативного признака. Например, группировка рабочих по факторному признаку х – квалификации (разряду) с указанием заработной платы, можно увидеть прямую зависимость результативного признака у – средней месячной заработной платы рабочих от квалификации: чем выше квалификация, тем выше и средняя месячная зарплата. При использовании в аналитических группировках методов математической статистики, можно определить показатель тесноты (силы) связи между изучаемыми признаками |
|
23 |
Метод комбинаторной группировки |
Предполагает, что группы, образованные по одному признаку, делятся затем на подгруппы по второму и т.д. признакам (т.е. в основании группировки лежит несколько признаков, взятых в комбинации) |
|
24 |
Метод многомерной группировки |
Позволяет рассматривать совокупность единиц одновременно по множеству характеризующих признаков и принимать управленческие решения с использованием теории распознавания образов. Многомерная группировка (многомерная классификация) основана на измерении сходства или различия между объектами: единицы, отнесенные к одной группе (классу) отличаются между собой меньше, чем единицы, отнесенные к разным группам (классам). Мерой близости (сходства) между объектами могут служить различные критерии. Самая распространенная мера близости – евклидово расстояние между объектами, представленными точками в n-мерном пространстве. Задача многомерной группировки – выделение сгущений точек (т.е. близости по всему комплексу признаков) – кластерный анализ |
|
25 |
Метод первичной группировки |
Связан с определением оптимального количества групп с равными интервалами, при условии, что распределение единиц совокупности близко к нормальному, можно по формуле американского ученого Стерджесса: n=1+3,322*lgN, где N – число единиц совокупности. Величина интервала для группировок с равными интервалами: i |
|
26 |
Метод вторичной группировки |
Применяется в тех случаях, когда имеющиеся первичные группировки не удовлетворяют требованиям анализа. Например, по причине несопоставимости группировок из-за различного числа выделенных групп или неодинаковых границ интервалов. Метод вторичной группировки позволяет привести такие исходные группировки к сопоставимому виду для проведения их дальнейшего сопоставительного анализа. |
|
27 |
Балансовый способ |
Используется для отражения соотношений, пропорций двух взаимосвязанных и уравновешенных экономических показателей, итоги которых должны быть тождественными. В частности, этот способ используется при проверке правильности определения влияния различных факторов на прирост величины результативного показателя. При детерминированном анализе алгебраическая сумма величины влияния отдельных факторов должна соответствовать величине общего прироста результативного показателя (∆Yобщ=∑∆Yi). При этом влияние каждого i-го фактора на изменение общего результата ∆Yобщ можно описать в виде: ∆Yа= Yа-Y0 ∆Yb= Yb-Yа ∆Yc= Yc-Yb ∆Yd= Yd-Yc, и т.д. |
Характеристики методов принятия управленческих решений, на основе детерминированного факторного анализа, состав которых представлен в табл. 4, используемые в общем менеджменте при принятии управленческих решений при наличии полной и точной количественной информации, подробно рассмотрены в работе [23].
Таблица 4
Методы принятия управленческих решений на основе детерминированного факторного анализа, используемые в общем менеджменте
|
№ |
Метод ПУР |
Характеристика МПУР |
|
1 |
Метод цепных подстановок |
|
|
2 |
Индексный способ |
Основан на вычислении относительных показателей динамики, пространственных сравнений, выполнения плана (норматива, прогноза) и т.д. |
|
3 |
Метод абсолютных разниц |
Используется в мультипликативных и мультипликативно-аддитивных моделях и заключается в расчете величины влияния факторов умножением абсолютного прироста исследуемого фактора на базовую величину фактора, находящегося справа от него и на фактическую величину факторов, расположенных слева. Например, для мультипликативной факторной модели типа |
|
4 |
Метод относительных разниц |
Используется в мультипликативных и мультипликативно-аддитивных моделях для измерения влияния факторов на прирост результативного показателя. Он заключается в расчете относительных отклонений величин факторных показателей с последующим расчетом изменения результативного показателя Yф за счет каждого фактора относительно базового Yб. Например, для мультипликативной факторной модели типа |
|
5 |
Метод пропорционального деления (долевого участия) |
Используется для аддитивных Y=a+b+c и кратных моделей типа Y=a/(b+c+d), в том числе многоуровневых. Этот метод заключается в пропорциональном распределении прироста результативного показателя Y за счет изменения каждого из факторов между ними. Например, для аддитивной модели типа Y=a+b+c влияние факторов рассчитывается |
|
6 |
Метод дифференциального исчисления |
Предполагает, что общее приращение функции различается на слагаемые, где значение каждого из них определяется как произведение соответствующей частной производной на приращение переменной, по которой вычислена данная производная |
|
7 |
Метод простого прибавления неразложимого остатка |
Подразумевает равномерное распределение этого остатка между факторами |
|
8 |
Метод взвешенных конечных разностей |
Предполагает, что величина влияния каждого фактора определяется по каждому из вариантов подстановки факторов, после чего результаты суммируются и от полученной суммы берется средняя величина, дающая единый ответ о значении влияния фактора |
|
9 |
Логарифмический метод |
Заключается в логарифмически пропорциональном распределении остатка по искомым факторам и применяется в мультипликативных моделях. Результаты расчетов не зависят от местоположения факторов в модели |
|
10 |
Метод коэффициентов |
Основан на сопоставлении числовых значений одних и тех же базисных экономических показателей при разных условиях |
|
11 |
Интегральный метод |
Применяется для определения влияния факторов в мультипликативных, кратных и смешанных моделях кратно-аддитивного вида, позволяя получить более точные результаты вычисления влияния факторов по сравнению со способами цепной подстановки, абсолютных и относительных разниц и избежать неоднозначной оценки влияния |
В данном рассмотрении подробнее проанализируем возможности принятия управленческих решений с использованием методов на основе стохастического факторного анализа, состав и основные характеристики которых, используемых в общем менеджменте, представлены в табл. 5 [32].
Таблица 5
Методы принятия управленческих решений на основе стохастического факторного анализа, используемые в общем менеджменте
|
№ |
Метод ПУР |
Характеристика МПУР |
|
1 |
Метод корреляционного анализа |
Позволяет установить наличие и тесноту связи между факторами, определяющими результат управления |
|
2 |
Метод регрессионного анализа |
Позволяет установить аналитическую зависимость между воздействующими факторами и результирующим показателем при стохастической природе исследуемых признаков |
|
3 |
Метод кластерного анализа |
Как метод многомерного анализа предназначен для группировки (кластеризации) совокупности элементов по множеству признаков. Значения каждого из признаков служат координатами каждой единицы изучаемой совокупности в многомерном признаковом пространстве. Поскольку каждый наблюдаемый элемент характеризуется значениями нескольких показателей, его можно представить как точку в многомерном пространстве координат этих показателей. При этом основным критерием кластеризации является то, что различия между элементами разных кластеров должны быть более существенными, чем между элементами, отнесенными к одному кластеру |
|
4 |
Дисперсионный анализ |
Метод, основанный на технологиях математической статистики, направленный на поиск зависимостей в экспериментальных данных путём исследования значимости различий в средних значениях изучаемых величин, позволяя сравнивать средние значения множества групп. Применяется при принятии управленческих решений, когда характер зависимостей заранее неизвестен и требует проведения экспериментальных исследований |
Рассматривая метод регрессионного анализа, необходимо отметить, что при решении многих задач управления экономическими системами (рис. 2) [2] требуется получение ответа на вопросы:
– влияет ли тот или иной фактор (Х) на результат деятельности (Y) управляемой экономической системы? (да или нет),
– какова направленность этой связи (положительная или отрицательная),
– насколько велика степень этой связи? (сильная, средняя, слабая),
– каков характер этой связи? (линейная или нелинейная).

Рис. 2. Зависимость между результирующим экономическим показателем Y и воздействующим фактором Х
При этом нужно отметить, что для принятия управленческого решения мы, как правило, располагаем ограниченным объемом исходных данных, носящих вероятностный (стохастический) характер.
Иначе говоря, если в классическом детерминированном анализе каждому значению воздействующего фактора Х соответствует строго определенное значение результата YY, то при стохастическом анализе каждому значению фактора Х с различной степенью вероятности может соответствовать несколько значений показателя Y.
Поскольку на формирование результирующего показателя YYобычно оказывает влияние большое число факторов, носящих как закономерный, так и случайный характер, то в процессе дальнейшего анализа статистическую зависимость условно разделяют на две составляющие:
– неслучайную (детерминированную) основу в виде функциональной зависимости, характеризующей сложившуюся тенденцию связи между показателем YY и фактором Х;
– случайную компоненту, характеризующую разброс отдельных наблюдений относительно детерминированной основы.
Простейшую зависимость показателя YY от фактора Х выражает линейная однофакторная модель вида:
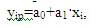
где yip – расчетное значение детерминированной основы показателя при заданном значении фактора xi,
a0 и a1 – cтатистические коэффициенты, получаемые путем обработки фактических данных о значениях определенной совокупности yi и xi.
Разница между фактическим значением показателя yi при фиксированном хi и расчетным значением детерминированной основы yip, именуемая случайной компонентой (остатком), определяется соотношением:
εi=yi-yip.
Расчетные значения yip находятся на линии регрессии, а фактические значения yiрасполагаются в некоторой области, прилегающей к этой линии.
Задача получения уравнения регрессии состоит в нахождении на основе пар наблюдений (xi,yi) таких значений коэффициентов a0 и a1, при которых линия регрессии пройдет максимально близко к точкам фактических наблюдений.
Наилучшим способом нахождения коэффициентов уравнения регрессии является метод наименьших квадратов, разработанный Гауссом и Лежандром, суть которого заключается в нахождении коэффициентов a0 и a1 для которых сумма квадратов разностей между фактическими значениями показателя yi и расчетными yip, лежащими на линии регрессии, минимальна  .
.
Часто для удовлетворения потребностей практики используются многофакторные линейные модели, обладающие простотой получения и ясностью экономической интерпретации.
Линейная многофакторная модель имеет вид:
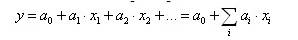
Для расчета статистических коэффициентов уравнения регрессии a также используется метод наименьших квадратов.
также используется метод наименьших квадратов.
Если на показатель y наибольшее влияние оказывает один фактор x, но связь между ними носит нелинейный характер, то может быть использована однофакторная нелинейная модель (типа параболы) вида:
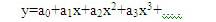
В случаях, когда на показатель y нелинейно влияет несколько факторов, могут быть использованы степенные
y=a0∙x1a1∙x2a2...,
показательные функции
y=a0∙a1x1∙a2x2...
и иные варианты моделей.
Выбор вида модели при анализе, наилучшим образом характеризующей существо экономического процесса, предполагает выполнение следующей последовательности рекомендаций [2]:
1) провести качественный отбор факторов исходя из предположения о возможном их влиянии на анализируемый показатель;
2) собрать и систематизировать данные о значениях показателя и факторов по таблице-матрице: «m факторов – n опытов»;
3) провести графический анализ связи между показателем и каждым фактором, позволяющим предварительно установить наличие связи и ее вид (возрастающая или убывающая, прямолинейная или криволинейная функция);
4) построить регрессионную модель. При этом, если графический анализ не позволяет однозначно выбрать вид модели, то следует использовать одну и ту же статистику для получения различных уравнений (линейных и нелинейных, однофакторных и многофакторных) и сравнить их между собой по одному из известных критериев, например, по методу наименьших квадратов:
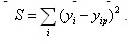 .
.
Еще одним из критериев эффективности уравнения регрессии является относительная погрешность εотн. Если рассматривать относительную погрешность εотн при использовании, например, линейного уравнения по сравнению с уравнением параболы, то она будет выражена соотношением:
εотн =(Sл-Sп)/Sл,
где Sл – сумма квадратов отклонений фактических значений от расчетных по линейной модели,
Sп – сумма квадратов отклонений фактических значений от расчетных по параболической модели.
Относительная погрешность εотн дает возможность соотнести точности используемых регрессионных зависимостей относительно друг друга, но не отвечает на вопрос, насколько эти уравнения регрессии близки к истинным значениям.
Ответ на этот вопрос может быть дан другим критерием приемлемости уравнения регрессии – средней относительной ошибкой εср, определяемой как отношение суммы абсолютных значений отклонений фактических значений от расчетных к сумме всех фактических значений показателя:
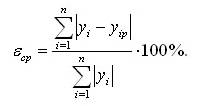
На практике принято считать, что если величина εср≤15%, то модель считается адекватной реальному процессу.
Для оценки соответствия уравнения регрессии реальной статистике часто используется критерий Фишера F, определяемый по формуле:
σ2рег
Fрасч = ───,
σ2ост
где σ2рег – дисперсия регрессии, характеризующая отклонения расчетных значений показателя от его среднего значения:
n_ n _
Σ(yip-y)2 Σ(yip-y)2
i=1 i=1
σ2рег=───────── = ─────────,
fрегm-1
где n – количество пар наблюдений yi и xi;
m – число вычисляемых статистических параметров (а0,а1,а2,...);
σ2ост – остаточная дисперсия, характеризующая отклонения фактических значений показателя y от расчетных, полученных с помощью уравнения регрессии:
n n
Σ(yi-yip)2 Σ(yi-yip)2
i=1 i=1
σ2ост=───────── = ─────────
fостn-m
Величина σ2рег характеризует интенсивность изменения показателя при варьировании фактора, а значение σ2ост – плотность расположения точек относительно уравнения регрессии.
Расчетное значение F-критерия (Fрасч) сравнивается с табличным (Fтабл). При Fрасч>Fтабл гипотеза об адекватности проверяемого уравнения регрессии принимается, в противном случае – отвергается. При этом учитывается степень гарантии, с которой можно принять гипотезу о возможности использования проверяемого уравнения регрессии.
Экономический смысл коэффициентов уравнения регрессии рассмотрим на примере линейной однофакторной модели вида y=a0+a1x.
Величина коэффициент a0 характеризует [2]:
– существование помимо х других факторов, оказывающих влияние на результирующий показатель у;
– наличие большого количества случайных факторов, оказывающих влияние результирующий показатель у;
– недостаточность исходных статистических данных для определения формы зависимости между х и у.
Величина коэффициента a1 характеризует степень изменения результирующего показателя у при варьировании исследуемого воздействующего фактора х.
Метод корреляционного анализа позволяет установить тесноту связи между воздействующими факторами и результирующими показателями. Оценка степени влияния на изменение результирующего показателя каждого фактора, позволяющая формировать мероприятия для достижения требуемых значений выходных показателей осуществляется с помощью корреляционного анализа.
Простейшая мера связи между показателем у и фактором х – функция S, используемая в методе наименьших квадратов:
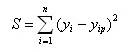
Другой мерой связи является среднее значение квадратов остатков, т.е.
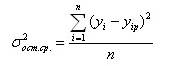
Соотношение σ2ост.ср./σ2у характеризует уменьшение размаха колебаний фактических значений результирующего показателя у в результате использования линии регрессии. Если соотношение σ2ост.ср./σ2у=0, то это значит, что все точки выборки лежат на линии регрессии (т.е. зависимость между показателем и фактором носит строго функциональный характер). Если соотношение σ2ост.ср./σ2у=1, то уравнение регрессии ничего не объясняет [2].
Таким образом, отношение σ2ост.ср./σ2у характеризует долю дисперсии показателя у, необъясненную регрессионной моделью, построенной с использованием фактора х.
Иным показателем, характеризующим улучшение качества модели (повышение тесноты связи между х и у) с возрастанием его значения является коэффициент детерминации:
R2=1-(σ2ост.ср./σ2у)=1-Σ(yi-yip)2/Σ(yi-ycp)2,
характеризующий ту долю совокупной дисперсии σ2у, которая объясняется с помощью регрессионной модели. При R2=1 все значения выборки лежат на линии регрессии. При R2=0 уравнение регрессии ничего не объясняет.
Основными достоинствами коэффициента детерминации являются:
– симметричность относительно Х и У, т.е. R2xy=R2yx;
– приемлемость как для однофакторной, так и для многофакторной модели любого вида;
– универсальность как меры качества подбора уравнения регрессии.
По аналогии между дисперсией и средним квадратическим отклонением в математической статистике, в регрессионном анализе вместо коэффициента детерминации используют индекс корреляции (или корреляционное отношение):
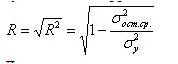
Для проверки наличия корреляции используют корреляционный момент (ковариацию) Кxy:
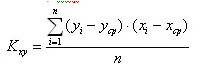
Значение Кxy=0 свидетельствует о том, что связь между х и у отсутствует. Если Кxy≠0, то связь между х и у есть.
Для оценки тесноты связи х и у используется и безразмерная величина – коэффициент парной корреляции rxy (отношение корреляционного момента Кxy к произведению средних квадратических отклонений показателя σy и фактора σx:
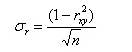 .
.
Таким образом, коэффициент парной корреляции rxy может меняться в пределах от +1 до -1 (для возрастающей и убывающей функций, соответственно) и равен нулю при отсутствии связи.
Коэффициент парной корреляции является мерой приближения к линейной функциональной связи. Для нелинейной функциональной связи между х и у rxy≠1.
Для оценки надежности коэффициента парной корреляции rxy определяется его погрешность по формуле:
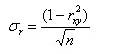
после чего определяется отношение rxy/σr.
Если rxy/σr>3, то можно считать, что полученный коэффициент корреляции отражает суть связи х и у (при n≥50).
Индекс корреляции Rxy и коэффициент парной корреляции rxy связаны между собой зависимостью Rxy≥rxy.
Если на показатель влияет не один фактор, а несколько, их влияние оценивается не через коэффициент парной корреляции, а через совокупный коэффициент корреляции, определяемый, например, для двух факторов (х1,х2) по формуле:
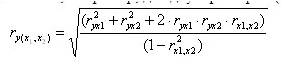
где ryx1,ryx2 – коэффициенты парной корреляции между показателем у и факторами х1,х2;
rx1,x2 – коэффициенты парной корреляции между факторами х1,х2.
Явление тесной связи факторов между собой в сложных процессах называется мультиколлинеарностью. Если rx1,x2>│0,8│, то это свидетельствует о мультиколлинеарности. В этом случае один из факторов следует исключить, так как он очевидно может быть выражен через другой. Выбор фактора осуществляется на основе качественного анализа процесса.
Совокупный коэффициент корреляции изменяется от 0 до 1. Если ry(x1,x2)=0, то показатель у не может быть связан с х1 и х2 линейной корреляционной зависимостью. При этом возможна другая связь. Если ry(x1,x2)=1, то значит связь между у,х1,х2 носит линейный функциональный характер. Во всех остальных случаях совокупный коэффициент корреляции – мера линейной корреляции между у, х1 и х2.
Если в уравнении регрессии более двух факторов, то совокупный коэффициент корреляции рассчитывается через определители:
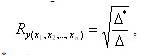
где ∆* и ∆ – определители:
1 , rx1x2, …,rx1xp, rx1y
∆*= rx2x1, 1, …,rx2xp, rx1y
… … … … …
rxpx1, rx2xp, …,1 , rxpy
rx1x2, 1, rx3x2, …,rxpx2
∆= rx1x3, rx2x3, 1, …,rxpx3
… … … … …
rx1xp, rx2xp, rx3xp, …,1
Частные коэффициенты корреляции представляют собой оценки степени связи показателя у с одним из факторов при исключении влияния других.
Метод кластерного анализа (от англ. cluster – гроздь, сгусток, пучок) как метод многомерного анализа предназначен для группировки (кластеризации) совокупности элементов по множеству признаков. Значения каждого из признаков служат координатами каждой единицы изучаемой совокупности в многомерном признаковом пространстве. Поскольку каждый наблюдаемый элемент характеризуется значениями нескольких показателей, его можно представить, как точку в многомерном пространстве координат этих показателей. При этом основным критерием кластеризации является то, что различия между элементами разных кластеров должны быть более существенными, чем между элементами исследуемой совокупности, отнесенными к одному кластеру.
Спектр применения метода кластерного анализа очень широк. Помимо задач управления (менеджмента) он активно используется в антропологии, археологии, биологии, геологии, информационных технологиях, маркетинге, медицине, психологии, социологии, химии, философии и других сферах.
Основные задачи, решаемые методом кластерного анализа, представлены на рис. 3.
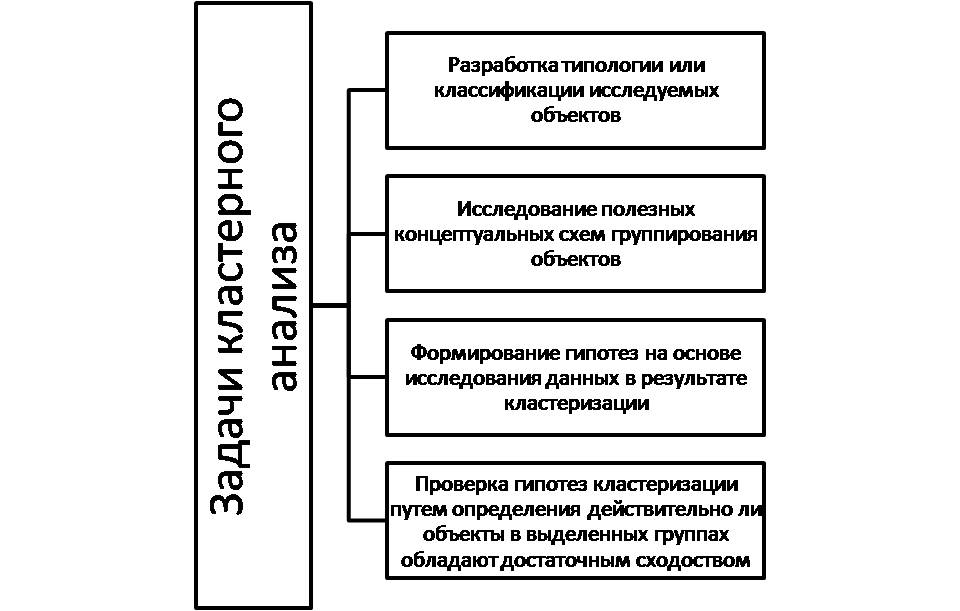
Рис. 3. Основные задачи, решаемые методом кластерного анализа
Реализация метода кластерного анализ независимо от объектов исследования предполагает последовательное выполнение следующих этапов действий:
– во-первых, формирование выборки для кластеризации, изначально предполагающее, что кластеризации подлежат только количественные данные;
– во-вторых, определение множества переменных, образующих признаковое пространство, по которым будут оцениваться объекты в выборке;
– в-третьих, вычисление значений той или иной меры сходства (или различия) между изучаемыми объектами;
– в-четвертых, формирование групп объектов, сходных по тем или иным признакам;
– в-пятых, проверка достоверности результатов формирования групп объектов.
Основными требованиями, предъявляемыми к объектам, исследуемым методом кластерного анализа, являются их однородность и полнота данных о них.
Требование однородности означает, что объекты, обрабатываемые методом кластерного анализа, должны быть одной природы и описываться сходным набором характеристик. Для предварительного отбора однородных объектов целесообразно использовать метод факторного анализа, который, кроме того, обеспечивает z-стандартизацию без негативных последствий для выборки (если её проводить непосредственно для кластерного анализа, она может повлечь за собой уменьшение чёткости разделения групп).
Требование полноты означает, что исследуемые объекты, должны описываться набором характеристик, именуемых признаками, достаточными для проведения кластерного анализа.
Признаки, описывающие объекты кластеризации, могут быть как числовыми, так и нечисловыми.
С использованием этих признаков формируются матрицы расстояния и матрицы сходства.
Матрица расстояния между объектами в кластерном анализе предполагает, что каждый объект в метрическом пространстве описывается расстоянием до других объектов.
Матрица сходства между объектами в кластерном анализе предполагает учет степени сходства рассматриваемого объекта в метрическом пространстве с другими объектами выборки.
В кластерном анализе используется несколько алгоритмов обработки входных данных:
– Q-тип анализа, предполагающий сравнение объектов исходя из их признаков;
– R-тип анализа, предполагающий сравнение признаков исходя из объектов;
– RQ-тип анализа, представляющий собой гибридный вариант анализа.
Основные цели кластеризации представлены в табл. 6.
Таблица 6
Основные цели кластеризации
|
№ |
Цель |
Содержание цели |
|
1 |
Понимание изучаемых данных |
Достигается путём выявления кластерной структуры, когда производится разбиение выборки на группы схожих объектов, что позволяет упростить дальнейшую обработку данных и принятия решений, применяя к каждому кластеру свой метод анализа (что соответствует стратегии «разделяй и властвуй»). При этом число кластеров стремятся минимизировать |
|
2 |
Сжатие данных |
Применяется, когда исходная выборка избыточно велика, и ее требуется сократить, оставив только наиболее типичных представителей от каждого кластера. При этом принципиально важно обеспечить высокую степень сходства объектов внутри каждого кластера, сколь много бы их не было выделено |
|
3 |
Обнаружение новизны |
Направлено на выделение с целью изучения нетипичных объектов, которые не подходят по своим признакам ни к одному из ранее выделенных кластеров |
Для достижения каждой из целей, представленной в табл. 6, может быть использована иерархическая кластеризация, когда крупные кластеры последовательно дробятся на более мелкие. Решение подобного рода задач, известных как задачи таксономии, обеспечивает формирование древообразной иерархической структуры, где каждый исследуемый объект характеризуется перечислением всех кластеров, которым он принадлежит, сверху вниз (от самого крупного кластера к самому мелкому).
Классификация методов кластеризации представлена в табл. 7
Таблица 7
Основные методы кластеризации
|
№ |
Группа методов |
Состав методов |
Характеристика методов |
|
1 |
Вероятностные методы |
Метод К-средних, Метод К-медиан, ЕМ – алгоритм, Метод алгоритмов FOREL, Метод дискриминационного анализа |
Разделяют исследуемые элементы рассматриваемого множества на основе определения уровня (степени) возможности наступления некоторого события в результате реализации некоторого изучаемого процесса |
|
2 |
Методы на основе систем искусственного интеллекта |
Метод нечеткой кластеризации на основе С-средних, Метод кластеризации с использованием нейронной сети Т. Кохонена, Метод кластеризации на основе генетического (эвристического) алгоритма |
Разделяют исследуемые объекты множества клиентов банка на основе признаков их сходства и различия в многомерном признаковом пространстве |
|
3 |
Логические методы |
Построение диаграммы специализированного вида, представляющей собой графическое изображение в двухмерной проекции степени подобия объектов, именуемой дендрограммой |
Формирование схемы логических взаимосвязей сотрудников банка с клиентами при предоставлении банковских услуг с использованием дерева решений |
|
4 |
Методы графов |
Методы графов включают достаточно широкий спектр способов построения (sortingstrategies), в том числе: – метод одиночной связи (singlelinkage) – «метод ближайшего соседа»; – метод полной связи (completelinkage) – «метод дальнего соседа»; – метод средней связи (pair-group method using arithmetic averages) – невзвешенный (unweighted) или взвешенный (weighted); – центроидный метод (pair-group method using the centroi daverage) – невзвешенный или взвешенный (медианный); – метод Уорда (Ward’smethod) |
Являются разновидностью геометрического подхода к изучению множества клиентов банка как объектов, в котором граф задаётся множеством вершин (точек), отражающим состояния клиентов банка, и множеством рёбер (связей), отражающих процессы взаимодействия сотрудников банка с клиентами, соединяющих пары вершин, возможно несколькими ребрами
|
|
5 |
Иерархические методы |
Предполагают алгоритмические исследования вложенных групп (кластеров) различного порядка, включающие подходы: – агломеративные (объединительные), – дивизивные (разделяющие) на основе таксономии, – монотетические (выделение по одному признаку), – политетические (выделение по множеству признаков) |
Позволяют провести сегментацию клиентов банка по группам, объединяя и разделяя их по одному или нескольким признакам потребительских предпочтений |
|
6 |
Специальные методы кластеризации |
Включают: – статистические алгоритмы кластеризации, – метод ансамбля кластеризаторов, – алгоритмы автоматической кластеризации (FOREL, KRAB, JOINT), – алгоритмы, основанные на методе просеивания, – методы классификации DBSCAN, обеспечивающие пространственное объединение объектов в кластеры по зашумленным плотностям распределения |
Позволяют сформировать перечень банковских услуг на основе исследования и группировки клиентских запросов и предпочтений |
Формальная постановка задачи кластеризации заключается в том, что для множества объектов Х и множества имен кластеров У задается функция расстояния между объектами 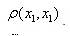 . Также задана обучающая выборка из mобъектов, удовлетворяющая условиям
. Также задана обучающая выборка из mобъектов, удовлетворяющая условиям 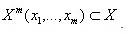 .
.
Задача заключается в том, чтобы разделить выборку на непересекающиеся подмножества, именуемые кластерами, так, чтобы каждый кластер состоял из объектов, близких по метрике 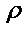 , а объекты разных кластеров существенно отличались. При этом каждому объекту
, а объекты разных кластеров существенно отличались. При этом каждому объекту  приписывается номер кластера
приписывается номер кластера 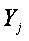 .
.
Сам алгоритм кластеризации представляет собой реализацию функции 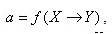 , которая любому объекту
, которая любому объекту 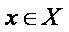 ставит в соответствие кластера
ставит в соответствие кластера 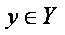 . Множество Y в некоторых случаях определено заранее, однако чаще ставится задача определить состав, признаки классификации и оптимальное число кластеров, с точки зрения того или иного критерия качества кластеризации.
. Множество Y в некоторых случаях определено заранее, однако чаще ставится задача определить состав, признаки классификации и оптимальное число кластеров, с точки зрения того или иного критерия качества кластеризации.
Принятию управленческих решений с использованием метода кластерного анализа присущи следующие особенности.
Во-первых, необходимо учитывать, что не существует однозначно наилучшего критерия качества кластеризации. Известен целый ряд эвристических критериев, а также ряд алгоритмов, не имеющих чётко выраженного функционала, но осуществляющих достаточно разумную кластеризацию «по построению». Использование этих подходов может давать разные результаты кластеризации. Поэтому для осуществления кластеризации целесообразно приглашать экспертов в предметных областях, которые помогут осуществить осмысленное выделение кластеров.
Во-вторых, поскольку число кластеров, как правило, заранее неизвестно и устанавливается в соответствии с некоторым субъективным критерием, выделение кластеров осуществляется за счёт формализованного подхода на основе мер близости, обеспечивающих вероятностную картину.
В-третьих, результат кластеризации существенно зависит от метрики, выбор которой, как правило, также субъективен и определяется на основе экспертных оценок.
Метод дисперсионного анализа направлен на поиск зависимостей в экспериментальных данных путём исследования значимости различий в средних значениях. Этот метод позволяет сравнивать средние значения нескольких групп переменных.
Разработанный для анализа результатов экспериментальных исследований метод дисперсионного анализа связан с изучением влияния одной или нескольких независимых переменных (факторов) на исследуемую зависимую переменную.
Независимые переменные, являясь номинативными, и характеризуясь шкалой наименований, отражают групповую принадлежность, то есть могут иметь две или более градации (или уровня).
Зависимые переменные в дисперсионном анализе представляются значениями абсолютных шкал, именуемых шкалами отношений.
Градации, соответствующие независимым выборкам объектов, называются межгрупповыми, а градации, соответствующие зависимым выборкам, – внутригрупповыми.
Классификация вариантов дисперсионного анализа в зависимости от типа и количества переменных различают, а также областей применения приведены в табл.8.
Таблица 8
Классификация вариантов дисперсионного анализа
|
№ |
Класс |
Область применения |
|
1 |
Однофакторный и многофакторный дисперсионный анализ |
Случай одной или нескольких независимых переменных |
|
2 |
Одномерный и многомерный дисперсионный анализ
|
Случай одной или нескольких зависимых переменных |
|
3 |
Дисперсионный анализ с повторными измерениями |
Случай зависимых выборок |
|
4 |
Дисперсионный анализ с постоянными факторами, случайными факторами, и с факторами обоих типов, представленных в смешанных моделях |
Случай постоянных, случайных факторов и их комбинаций |
Математическая модель дисперсионного анализа в общем виде представляет собой частный случай основной линейной модели, в которой с помощью методов 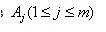 производится измерение нескольких параметров
производится измерение нескольких параметров  , чьи точные значения
, чьи точные значения
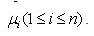 . Тогда в общем случае результаты измерений различных величин разными методами можно представить как:
. Тогда в общем случае результаты измерений различных величин разными методами можно представить как:
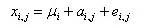
где:
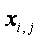 – результат измерения i-го параметра с помощью метода
– результат измерения i-го параметра с помощью метода 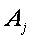 ;
;
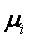 – точное значение i-го параметра;
– точное значение i-го параметра;
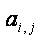 – систематическая ошибка измерения i-го параметра в группе с помощью метода
– систематическая ошибка измерения i-го параметра в группе с помощью метода 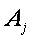 ;
;
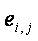 – случайная ошибка измерения i-го параметра с помощью метода
– случайная ошибка измерения i-го параметра с помощью метода 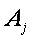 .
.
Процедура дисперсионного анализа заключается в определении для измеряемых данных соотношения систематической (межгрупповой) дисперсии к случайной (внутригрупповой) дисперсии. При этом в качестве показателя изменчивости используется сумма квадратов отклонения значений параметра от среднего SS (Sum of Squares). Общая сумма квадратов отклонения значений параметра от среднего SSобщ раскладывается на межгрупповую сумму квадратов отклонений SSмг и внутригрупповую сумму квадратов отклонений SSвг: SSобщ=SSмг+ SSвг.
Для осуществления дисперсионного анализа необходимо выполнение следующих условий.
Во-первых, это нормальное распределение зависимой переменной.
Во-вторых, это равенство дисперсий в сравниваемых генеральных совокупностях.
В-третьих, это случайный и независимый характер выборки.
Таким образом, рассмотренная система методов стохастического факторного анализа позволяет осуществлять принятие управленческих решений по следующему алгоритму (рис. 4).

Рис. 4. Алгоритм принятия решения с использованием системы методов стохастического факторного анализа
Таким образом, реализуя полный цикл этапов алгоритма принятия решения (рис. 4) система методов стохастического факторного анализа является самодостаточной, обеспечивая решения самого массового блока задач ПУР с использованием количественных исходных данных стохастической природы.
В сочетании с общенаучными методами, методами, основанными на традиционных способах обработки информации и принятия решений, методами на основе детерминированного факторного анализа, методы на основе стохастического факторного анализа образуют полную систему принятия решений в общем менеджменте (рис. 5).
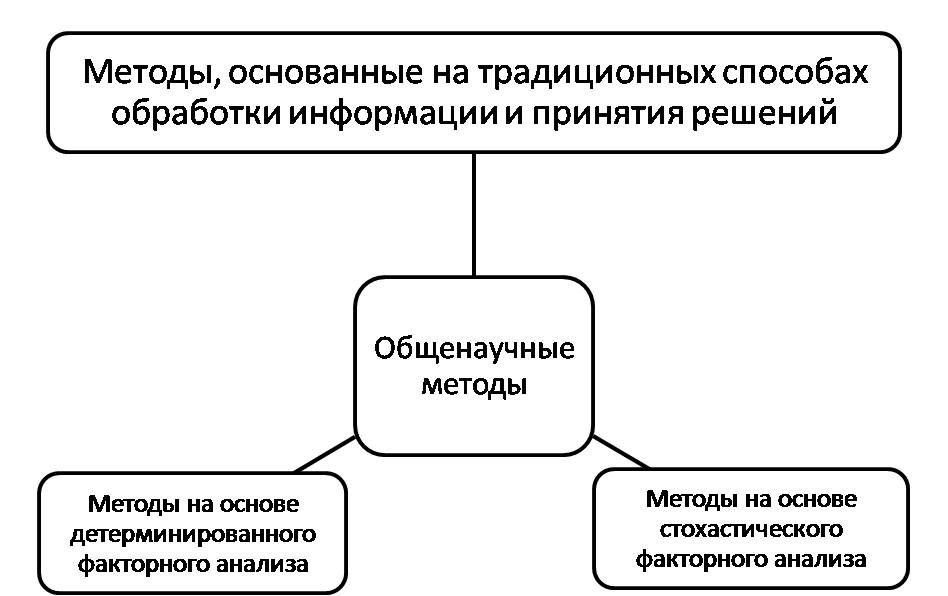
Рис. 5. Схема взаимосвязи общенаучных методов, методов, основанных на традиционных способах обработки информации и принятия решений, методов на основе детерминированного факторного анализа и методов на основе стохастического факторного анализа в системе общего менеджмента
В приведенной разработанной схеме системы принятия решений в общем менеджменте:
– общенаучные методы управления представляют собой методологическую базу для принятия решений;
– методы, основанные на традиционных способах обработки информации и принятия решений, обеспечивают предварительную обработку информации (подготовку процесса принятия решения);
– методы на основе детерминированного факторного анализа и методы на основе стохастического факторного анализа представляют собой альтернативные варианты методов решений, выбираемые в зависимости от качества (точности) получаемых после предварительной обработки сведений.
Представленная схема взаимосвязи методов принятия решений в системе общего менеджмента является:
– самодостаточной;
– инвариантной к специфике менеджмента той или иной организации;
– соответствующей инжиниринговому подходу, позволяющему добавлять в предложенную схему специализированные классы методов принятий решений, представленные в табл. 1.
1. Тебекин А.В., Тебекин П.А. Содержание общенаучных методов принятия управленческих решений в менеджменте. // Журнал исследований по управлению. - 2017. - Т. 3. - № 1. - С. 28-51.
2. Тебекин А.В. Методы принятия управленческих решений. - М.: Юрайт, 2016.
3. Балдин К.В., Воробьев С.Н., Уткин В.Б. Управленческие решения. - М.: ЮНИТИ-ДАНА, 2008. - 317с.
4. Гапоненко Т.В. Управленческие решения. - Р-н-Д: Феникс, 2012. - 284с.
5. Карданская Н.Л. Управленческие решения. - М.: ЮНИТИ-ДАНА, 2009. - 439 c.
6. Литвак Б.Г. Разработка управленческого решения. - М.: Дело, 2008. - 440 c.
7. Чудновская С.Н. Разработка управленческих решений. - Тюмень: ТГУ, 2009. - 304 с.
8. Тебекин А.В. Классификация методов принятия управленческих решений в менеджменте по областям применения. // Вестник Московского университета им. С.Ю. Витте. Серия 1: Экономика и управление. 2016. - № 4 (19). - С. 57-63.
9. Тебекин А.В., Касаев Б.С. Менеджмент организации. Учебник / А.В. Тебекин, Б.С. Касаев. Москва, 2014. (4-е издание).
10. Тебекин А.В. Менеджмент. - М.: ИНФРА-М, 2014.
11. Тебекин А.В. Управление инновационно-инвестиционной деятельностью в сфере информационных технологий: монография. - Москва: Палеотип, 2006. - 184 с.
12. Тебекин А.В. Теория менеджмента : учебник. - М. : КНОРУС, 2016. - 696 с.
13. Тебекин А.В. Теоретические основы управления инновационной деятельностью. Монография. Русайнс, 2016. - 213с.
14. Тебекин А.В. Теория управления. - М.: Кнорус, 2017. - 342 с.
15. Тебекин А.В., Тебекин П.А., Тебекина А.А. Использование информационно-технологической модели управления (ИТМУ) в принятии решений. // Вестник Московского университета им. С.Ю. Витте. Серия 1: Экономика и управление. - 2016. - № 1 (16). - С. 128-135.
16. Тебекин А.В. Логистика: учебник. Издание 2-е. - М.: Дашков и К, 2014. - 356 с.
17. Тебекин А.В. Управление качеством. - М.: Юрайт, 2013. - 384 с.
18. Тебекин А.В., Мантусов В.Б. Управление организацией: теоретико-методологические основы, функциональные задачи, технологии, прикладные аспекты применения. Монография. - Москва, 2016.
19. Тебекин А.В., Широкова Л.Н., Сурат И.Л. Управление инновационными проектами. Монография. - М.: Риалтекс, 2014. - 126с.
20. Тебекин А.В. Технологии экономического и таможенного риск-менеджмента как инструменты развития Евразийского экономического союза. В сборнике: Основные проблемы развития таможенного дела России в условиях ее членства в экономических интеграционных объединениях Сборник материалов Международной научно-практической конференции. Федеральная таможенная служба, ГКО ВПО "Российская таможенная академия". - 2015. - С. 31-37.
21. Тебекин А.В. Вопросы методологи и организации процесса управления социально-экономическим системами. // Инновационная экономика: информация, аналитика, прогнозы. 2017.
22. Тебекин А.В., Тебекин П.А. Методы принятия управленческих решений на основе традиционных способов анализа и обработки информации. // Журнал исследований по управлению. - 2017. - Т. 3. - № 2. - С. 1-25.
23. Тебекин А.В., Тебекин П.А., Тебекина А.А. Методы принятия управленческих решений на основе детерминированного факторного анализа. // Журнал исследований по управлению. - 2017. - Т. 3. - № 2. - С. 1-25.
24. Анисимов В.Г., Анисимов Е.Г., Блау С.Л., Мантусов В.Б., Новиков В.Е., Петров В.С., Тебекин А.В., Тебекин П.А. Управление инновациями. Монография. Под ред. проф. А.В.Тебекина / Государственное казенное образовательное учреждение высшего образования «Российская таможенная академия». Москва, 2017.
25. Тебекин А.В., Анисимов В.Г., Анисимов Е.Г., Петров В.С., Родионова Е.С., Сауренко Т.Н., Тебекин П.А. Теоретические основы управления инновациями. Научная монография. Под ред. проф. Тебекина А.В. - СПб.: Стратегия будущего, 2016. - 474с.
26. Тебекин А.В., Тебекина А.А. Классификация методов принятия управленческих решений. // Журнал исследований по управлению. - 2016. - Т.2. - №11. - С. 4.
27. Тебекин А.В. Мировые тенденции и национальные перспективы развития маркетинга и логистики как прикладных сфер управления. // Управленческие науки в современном мире. - 2015. - Т. II. - № 1. - С. 375-380.
28. Тебекин А.В., Збировская Е.П., Тебекин П.А. Принципы прикладного менеджмента: реализация информационных технологий управления. // Вестник РГГУ. Серия: Экономика. Управление. Право. -2016. - № 2 (4). - С. 86-94.
29. Тебекин А.В., Тебекин П.А. Прединвестиционная фаза проектного цикла по модели UNIDO как элемент методической базы разработки и реализации инновационных проектов и программ. // Вестник Московского университета им. С.Ю. Витте. Серия 1: Экономика и управление. 2016. - № 3 (18). - С. 97-107.
30. Тебекин А.В., Тебекин П.А. Общенаучные методы в системе классификации методов принятия управленческих решений в менеджменте. Маркетинг и логистика. - 2016. - № 6 (8). - С. 91-106.
31. Тебекин А.В. Признаковое пространство классификации методов принятия управленческих решений. // Инновационная экономика: информация, аналитика, прогнозы. - 2016. - № 4. - С. 34-39.
32. Тебекин А.В. Направления развития методов принятия управленческих решений прикладного менеджмента: общий менеджмент. // Журнал исследований по управлению. 2017.







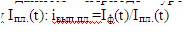
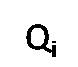 i
i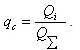
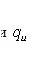

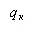





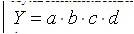 изменение величины влияния каждого фактора на результативный показатель определяется из выражений
изменение величины влияния каждого фактора на результативный показатель определяется из выражений


