Москва, г. Москва и Московская область, Россия
Москва, г. Москва и Московская область, Россия
В центре внимания статьи методические особенности обучения экстремальным задачам в высшей экономической школе, учет которых в практике преподавания математических дисциплин будет способствовать повышению качества математической и профессиональной подготовки выпускника экономического университета. Прикладные задачи социально-экономической тематики на определение наибольших и наименьших значений с методической точки зрения можно характеризовать как трудные задачи интегративного характера. Они представляют особый интерес в контексте усиления прикладной направленности обучения математике и актуализации новых приемов и активных методов обучения, как на уровне средней школы, так и для подготовки бакалавров в экономических университетах. В статье раскрыты затруднения студентов, возникающие в процессе решения этих прикладных задач. С содержательной точки зрения они объяснены трудностями формализации, предполагающей переход от реальной социально-экономической ситуации, описанной вербально, к соответствующей математической модели. Представлен фрагмент системы экстремальных задач, направленной на формирование понятий в области теории экстремальных задач, а также методов решения и принципов построения экстремальных задач и принципов формализации социально-экономических проблем в виде экстремальных задач.
математическая подготовка, методические особенности, прикладное усиление, условный экстремум, экономическая ситуация, экстремальная задача, экстремум.
Практика реализации прикладной математической подготовки будущих бакалавров, основные идеи которой представлены ранее в работах авторов [3, 4] свидетельствует о том, что процесс моделирования требует от студентов две важные компетенции: во-первых, адекватный перевод языка прикладной задачи на математический язык с возможностью обратного перевода, во-вторых, содержательную интерпретацию в терминах социально-экономической ситуации полученного результата внутримодельного исследования, записанного на формальном математическом языке. С методической точки зрения представляет большой интерес исследование процесса нахождения необходимого «языка», определяемого современной математической теорией, в частности дифференциальным исчислением функций нескольких переменных. Среди трудностей решения прикладных задач социально-экономической тематики отметим непонимание информации, подлежащей определению в процессе решения задачи. Реализуемая авторами методика усиления прикладной направленности обучения математике в экономическом университете подразумевает особое внимание к прикладным задачам социально-экономической тематики, в частности, задачам на условный экстремум. Данная статья посвящена раскрытию методических особенностей и теоретических основ рассматриваемого вида задач.
Задачи на наибольшее или наименьшее значение, связанные с методами оптимальных решений [11], относятся к разделу «Применение производной к исследованию функции одной переменной». Однако, если посмотреть на эти задачи с точки зрения теории функции многих переменных, то фактически любой сюжет задачи на наибольшее или наименьшее значение описывает некоторую величину, являющуюся функцией нескольких переменных, которые, если пользоваться соответствующей терминологией, удовлетворяют некоторой системе уравнении связи (или одному уравнению связи в частном случае). Отметим, что уравнений связи в системе на одно меньше, чем переменных. Но в отличие от задач на нахождение условного экстремума в теории функции многих переменных, система уравнении связи в рассматриваемых задачах всегда позволяет явно выразить все переменные через одну из них (независимую переменную, пробегающую некоторый промежуток), а это, в свою очередь, позволяет свести исследование функции нескольких переменных к исследованию функции одной независимой переменной на некотором множестве. Это множество также определяется (явно или неявно) условиями задачи. Учитывая вышесказанное, можно выделить важную методическую особенность – последовательность действий алгоритмического типа, которая с одной стороны является средством решения задач данного класса, с другой – средством интуитивного осмысления элементов новой математической теории, а с третьей стороны – средством обучения студентов решению прикладных экстремальных задач.
Итак, решение текстовых задач на нахождение наибольшего или наименьшего значения функции можно разбить на следующие три этапа: первый этап – составление математической модели реальной ситуации; второй этап – исследование полученной модели; третий этап – возврат к реальной ситуации и ответ на поставленный в экстремальной задаче вопрос. Можно выделить следующую общую содержательно-методическую особенность. «Если ищется максимум или минимум некоторой функции многих переменных при условии, что между этими переменными имеется связь, задаваемая одним или несколькими уравнениями, нужно прибавить к функции, экстремум которой мы ищем, функции, задающие уравнения связи, умноженные на неопределенные множители, и искать затем максимум или минимум построенной суммы, как если бы переменные были независимы. Полученные уравнения, присоединенные к уравнениям связи, послужат для определения всех неизвестных. Ж. Лагранж» [19].
Под оптимизацией в современных исследованиях принято понимать процесс определения наилучших или оптимальных решений разнообразных прикладных задач [16], как правило, связанных с исследованием социально-экономических ситуаций, а также производственных проблем, бизнес-задач и др. Оптимизация предполагает использование специальных математических моделей и методов. В качестве проблемы оптимизационной задачи выступает минимизация или максимизация значений критерия, значения которого заданы на множестве допустимых решений. Среди наиболее часто используемых критериев отметим доход, затраченное время, риск, фактическую продолжительность, эффективность, качество, стоимость и др. Важную роль в оптимизационной задаче играет учет заданных условиями реальной ситуации ограничений, которые могут быть записаны в виде уравнения или неравенства, а также системы уравнений, неравенств.
Задачи на поиск оптимальных значений функции постоянно возникают в практической деятельности, в том числе, в процессе решения сложных технических и социально-экономических задач [9, 17]. Это объясняется существованием возможности изменения параметров системы. Центральное место в прикладной математической подготовке будущего бакалавра экономики занимают классические методы оптимизации, накладывающие определённые ограничения на целевую функцию. Среди этих ограничений отметим выпуклость целевой функции, аналитическое задание целевой функции и возможность определения координат вектор-градиента в любой точке множества допустимых решений.
Однако в последние годы интерес исследователей смещается в сторону новых задач оптимизации, постановка и методы решения которых не в полной мере вписывается в классические рамки. Технический прогресс и изменение производства стали причинами появления новых оптимизационной задач, свойствами которых стали алгоритмическое задание функции, присутствия большого числа локальных экстремумов целевой функции, большая размерность оптимизационных задач и различные типы входящих параметров. Так, оптимизационная задача может одновременно содержать логические, целочисленные и вещественные параметры. В таких условиях возникает необходимость применения эволюционных методов оптимизации [7] и имитационного моделирования [6].
В учебном пособии [14] представлены основные приёмы, позволяющие находить оптимальные решения в различных задачах на поиск экстремумов функций нескольких переменных. При этом особое внимание уделяется обоснованию приемов и методов, в основе которых лежат необходимые и достаточные условия существования экстремума функций нескольких переменных. «Изложены численные методы нулевого, первого и второго порядков решения задач безусловной минимизации, а также численные методы поиска условного экстремума. Описаны алгоритмы решения задач линейного программирования, целочисленного программирования, транспортных задач. Приведены методы решения задач поиска безусловного и условного экстремума функционалов на основе метода вариаций». В учебном пособии [10] отмечается, что «практические задачи прикладной математики обладают рядом особенностей, среди которых – большая размерность (бесконечномерность), дискретность искомых переменных, стохастичность условий и другие особенности». В учебном пособии представлен ряд наиболее эффективных приемов и методов оптимизации сюжетных прикладных задач и классические алгоритмы для их решения.
Рассматривая связь исследования операций с классическими экстремальными задачами в своей исследовании [18] Хемди Таха отметил, что «Исследование операций ориентировано на решение практических задач, которые можно описать с помощью математической модели». Данное исследование содержит базовые разделы исследования операций, среди которых линейное программирование, нелинейное программирование, детерминированное программирование и стохастическое программирование, а также элементы теории принятия решений и введение в теорию игр. С методической точки зрения большой интерес представляет учебное пособие [12], специально разработанное авторами для усиления прикладной экономической направленности в области подготовки будущего учителя математики. Идеи реализации задачного подхода в преподавании математических дисциплин представлены в методологии проектирования учебного курса [13]. Представим далее четыре типовые задачи учебной темы «Условный экстремум функций нескольких действительных переменных» с решениями и соответствующими методическими комментариями.
Типовая задача 1. Функция полезности имеет вид  . Стоимости единиц первого блага x и второго блага y составляют 5 и 2 у.е. соответственно. На приобретение этих благ планируется затратить 900 у.е. Как распределить имеющуюся сумму затрат на приобретение благ, чтобы полезность была максимальной?
. Стоимости единиц первого блага x и второго блага y составляют 5 и 2 у.е. соответственно. На приобретение этих благ планируется затратить 900 у.е. Как распределить имеющуюся сумму затрат на приобретение благ, чтобы полезность была максимальной?
Решение. Рассмотрим функцию полезности  . Далее составим уравнение связи, учитывающее, что стоимости единиц первого блага x и второго блага y составляют 5 и 2 у.е. соответственно, а на приобретение этих благ планируется затратить 900 у.е. Получаем, что уравнение связи в этой экстремальной задаче имеет вид уравнения
. Далее составим уравнение связи, учитывающее, что стоимости единиц первого блага x и второго блага y составляют 5 и 2 у.е. соответственно, а на приобретение этих благ планируется затратить 900 у.е. Получаем, что уравнение связи в этой экстремальной задаче имеет вид уравнения  . Перейдем к составлению функции Лапласа на основе заданной функции полезности и составленного уравнения связи:
. Перейдем к составлению функции Лапласа на основе заданной функции полезности и составленного уравнения связи: 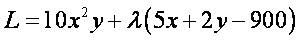 . Воспользовавшись необходимым условием существования экстремума, получим систему уравнений
. Воспользовавшись необходимым условием существования экстремума, получим систему уравнений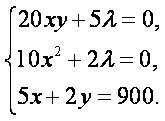 Данная система имеет единственное решение
Данная система имеет единственное решение 
Отметим, что полученное решение  – количество единиц блага каждого блага. Следовательно, функция полезности
– количество единиц блага каждого блага. Следовательно, функция полезности 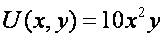 в точке
в точке 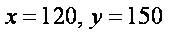 достигает максимума, т.е.
достигает максимума, т.е.  .
.
Методический комментарий. Опорными понятиями для первой типовой задачи являются: «Благо», «Дифференцирование произведения», «Достаточное условие экстремума», «Множитель Лагранжа», «Необходимое условие экстремума», «Полезность», «Решение системы уравнений», «Система уравнений», «Уравнение связи», «Функция Лагранжа», «Функция полезности», «Функция», «Частная производная», «Экстремум функции».
Типовая задача 2. Общие издержки производства задаются функцией  , где x и y соответственно количество товаров A и B. Общее количество произведенной продукции составило 120 единиц. Определите, сколько единиц товара каждого вида нужно производить, чтобы издержки были минимальны?
, где x и y соответственно количество товаров A и B. Общее количество произведенной продукции составило 120 единиц. Определите, сколько единиц товара каждого вида нужно производить, чтобы издержки были минимальны?
Решение. При нахождении условного минимума функции  следует записать уравнение связи. Учитывая, что по условию задачи общее количество произведенной продукции составило 120 единиц, получаем x+y=120. Следовательно, функция Лагранжа принимает вид
следует записать уравнение связи. Учитывая, что по условию задачи общее количество произведенной продукции составило 120 единиц, получаем x+y=120. Следовательно, функция Лагранжа принимает вид  , где x и y соответственно количество товаров A и B,
, где x и y соответственно количество товаров A и B, 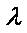 – коэффициент Лагранжа. Вычислим частные производные первого порядка:
– коэффициент Лагранжа. Вычислим частные производные первого порядка:

Таким образом, необходимо условие существования экстремума функции  принимает вид
принимает вид
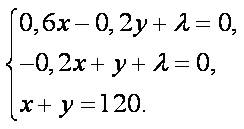
Решая полученную систему уравнений, получим 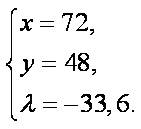
Таким образом, оптимальное количество товаров каждого вида A и B, которое следует производить с целью минимизации издержек производства равно A и B соответственно. Отметим, что при таких значениях количества товаров каждого вида общие издержки производства, заданные по условию задачи функцией  , будут равны
, будут равны 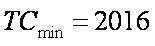 д.е.
д.е.
Методический комментарий. Опорными понятиями для второй типовой задачи являются: «Дифференцирование суммы», «Достаточное условие экстремума», «Множитель Лагранжа», «Необходимое условие экстремума», «Продукция», «Производство», «Решение системы уравнений», «Система уравнений», «Товар», «Уравнение связи», «Формула дифференцирования степенной функции», «Функция издержек», «Функция Лагранжа», «Функция», «Частная производная», «Экстремум функции».
Типовая задача 3. Производственная функция равна  , где x и y – количество единиц первого и второго ресурсов соответственно. Стоимость единицы первого ресурса составляет 5 у.е., а второго ресурса – 1 у.е. Бюджетное ограничение на ресурсы составляет 400 у.е. Какова будет максимальная прибыль при использовании этих ресурсов?
, где x и y – количество единиц первого и второго ресурсов соответственно. Стоимость единицы первого ресурса составляет 5 у.е., а второго ресурса – 1 у.е. Бюджетное ограничение на ресурсы составляет 400 у.е. Какова будет максимальная прибыль при использовании этих ресурсов?
Решение.

Методический комментарий. Опорными понятиями для третьей типовой задачи являются: «Бюджетное ограничение», «Достаточное условие экстремума», «Множитель Лагранжа», «Необходимое условие экстремума», «Прибыль», «Производственная функция», «Ресурс», «Решение системы уравнений», «Система уравнений», «Степенная функция», «Стоимость», «Уравнение связи», «Функция Лагранжа», «Функция», «Частная производная», «Экстремум функции».
Типовая задача 4. Фабрика выпускает два вида товара в объеме x и y соответственно. От реализации единицы товара x фабрика получает 8 у.е., а от единицы товара y – 10 у.е. Функция издержек имеет вид  . Сколько единиц товара каждого вида нужно производить, чтобы доход был максимальным, если на все издержки выделено 4400 у.е.? Найдите максимальное значение дохода.
. Сколько единиц товара каждого вида нужно производить, чтобы доход был максимальным, если на все издержки выделено 4400 у.е.? Найдите максимальное значение дохода.
Решение.

Методический комментарий. Опорными понятиями для третьей типовой задачи являются: «Достаточное условие экстремума», «Доход», «Издержки», «Множитель Лагранжа», «Необходимое условие экстремума», «Правила дифференцирования», «Решение системы уравнений», «Система уравнений», «Товар», «Уравнение связи», «Функция издержек», «Функция Лагранжа», «Функция», «Частная производная», «Экстремум функции».
Выделенные содержательные и методические особенности экстремальных задач, а также учитывающая эти особенности система задач, фрагмент которой представлен в данной статье, способствуют:
- формированию понятий в области теории экстремальных задач, а также методов решения и принципов построения экстремальных задач [5]; принципов формализации социально-экономических проблем и ситуаций в виде экстремальных задач;
- развитию экономического мышления и финансовой грамотности студентов [2], реализации интегративного подхода к проведению занятий по математическим дисциплинам, идеи которого представлены в работах [1, 8];
- использованию основных методов теории экстремальных задач, применяемых для исследования социально-экономических проблем и ситуаций, применению аналитических методов и методов вычислительной математики [15] дифференциального исчисления к решению типовых экстремальных задач;
- усвоению общих приёмов работы над прикладной задачей, совершенствование приемов и методов решения типовых экстремальных задач; знакомству с основными идеями и приёмами теории экстремальных задач на основе дифференциального исчисления функций нескольких переменных;
- развитию интереса и ознакомительного, изучающего чтения специальной литературы по математическому анализу и прикладной математике (математических методов в экономике), потребностей в использовании социально-экономических данных для построения и решения экстремальных задач.
1. Быканова О.А. О Подходе интеграции обучения математике и экономическим дисциплинам по летним школьным программам [Текст] / О.А. Быканова, Н.В. Филипова // Инновации и инвестиции. - 2015. - № 5. - С. 159-162. EDN: https://elibrary.ru/UWOJXL
2. Быканова О.А., Филиппова Н.В. Экономическое мышление и финансовая грамотность как составные элементы профильной направленности школьной математики для абитуриентов и учащихся на летней практике в экономическом ВУЗЕ [Текст] / О.А. Быканова, Н.В. Филипова / В сборнике: Проблемы и перспективы развития образования Материалы VI Международной научной конференции. - 2015. - С. 249-251. EDN: https://elibrary.ru/TREKZJ
3. Власов Д.А. Возможности профессиональных математических пакетов в системе прикладной математической подготовки будущих специалистов [Текст] / Д.А. Власов // Вестник Российского университета дружбы народов. Серия: Информатизация образования. - 2009. - № 4. - С. 52-59. EDN: https://elibrary.ru/KYATIX
4. Власов Д.А. Особенности целеполагания при проектировании системы обучения прикладной математике [Текст] / Д.А. Власов // Философия образования. - 2008. - № 4. - С. 278-283. EDN: https://elibrary.ru/KTXGOR
5. Власов Д.А. Математические модели и методы внутримодельных исследований: моногр. [Текст] / Д.А. Власов, Н.В. Монахов, М.В. Монахов - М., Альфа - 2007. - 365 с. EDN: https://elibrary.ru/QJSMFT
6. Власов Д.А. Дидактические особенности применения пакета имитационного моделирования ITHINK в системе подготовки бакалавров экономики [Текст] / Д.А. Власов, А.В. Синчуков / В сборнике: Современные информационные технологии и ИТ-образование Сборник научных трудов. Московский государственный университет имени М.В. Ломоносова, факультет вычислительной математики и кибернетики; Под редакцией В.А. Сухомлина. - 2015. - С. 295-299. EDN: https://elibrary.ru/WFXPIB
7. Горемыкина Г.И. Simulink-моделирование процессов экспресс-кредитования [Текст] / Г.И. Горемыкина, Н.А. Щукина // Моделирование, оптимизация и информационные технологии. - 2017. - № 4 (19). - С. 14. EDN: https://elibrary.ru/VVACIH
8. Калинина Е.С. Интегративный подход к проведению занятий по математическим дисциплинам в Вузах МЧС России [Текст] / Е.С. Калинина // Научно-аналитический журнал Вестник Санкт-Петербургского университета Государственной противопожарной службы МЧС России. - 2017. - № 2. - С. 187-193. EDN: https://elibrary.ru/ZRPWUP
9. Калинина Е.С. Применение математических методов в задачах проектирования сложных технических систем [Текст] / Е.С. Калинина / В сборнике: Фундаментальные и прикладные исследования: гипотезы, проблемы, результаты сборник материалов I Международной научно-практической конференции. - 2017. - С. 64-69. EDN: https://elibrary.ru/ZNLEND
10. Колбин В.В. Специальные методы оптимизации. [Текст] / В.В. Колбин / - Спб.: Лань, 2014. - 384 с. EDN: https://elibrary.ru/TXPHUF
11. Мастяева И.Н., Горемыкина О.Н. Методы оптимальных решений. [Текст] / И.Н. Мастяева, О.Н. Горемыкина /- ИНФРА- М, 2016. - 384 с. EDN: https://elibrary.ru/VQSKTZ
12. Монахов В.М. Методы оптимизации. Применение математических методов в экономике. [Текст] / В.М. Монахов, Э.С. Беляева, Н.Я. Краснер / - М.: Просвещение, 1978. - 175 с.
13. Муханов С.А. Проектирование учебного курса [Текст] / С.А. Муханов, А.И. Нижников // Педагогическая информатика. - 2014. - № 4. - С. 39-46. EDN: https://elibrary.ru/TJYTOT
14. Пантелеев А. В. Методы оптимизации в примерах и задачах. [Текст] / А.В. Пантелеев, Т.А. Летова / - Спб.: Лань, 2015 - 512 с. EDN: https://elibrary.ru/WMQAPT
15. Пантина И.В. Вычислительная математика - Московский финансово-промышленный университет «Синергия». [Текст] / И.В. Пантина, А.В. Синчуков / - 2012. - 176 с.
16. Синчуков А.В. Методические особенности математической подготовки бакалавра в экономическом университете [Текст] / А.В. Синчуков // Постулат. - 2017. - № 8 (22). - С. 19. EDN: https://elibrary.ru/ZFPWUH
17. Сухорукова И.В. Компьютерное моделирование и математическое обеспечение экономико-социальных задач [Текст] / И.В. Сухорукова, Г.Г. Лихачев // Экономический анализ: теория и практика. - 2003. - № 5. - С. 60-62. EDN: https://elibrary.ru/HYTRSJ
18. Таха Х. Исследование операций. [Текст] / Х. Таха /- М.: Вильямс, 2016. - 912 с.
19. Тихомиров В.М. Рассказы о максимумах и минимумах. [Текст] / В.М. Тихомиров /- М.: МЦНМО, 2006. - 200 с.






