Новочеркасск, Ростовская область, Россия
Новочеркасск, Ростовская область, Россия
Новочеркасск, Ростовская область, Россия
с 01.01.2019 по настоящее время
Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова (Общеинженерные дисциплины, профессор)
с 01.01.1980 по 01.01.2019
Москва, г. Москва и Московская область, Россия
ББК 308 Монтаж, эксплуатация, ремонт машин и промышленного оборудования
В статье рассматриваются уравнения двумерного потока воды, которая течет из безнапорных труб прямоугольного или круглого сечения. Для упрощения задачу, реальный трехмерный поток моделируется как двумерная зона с постоянными скоростями и ускорением жидкости в направлении, перпендикулярном зоне потока. Для описания закона движения потока воды используются уравнения Л. Эйлера для идеальной жидкости с учетом уравнений неразрывности и уравнения Бернулли. Модели двумерного потока в зоне распространения с достаточной для практики степенью адекватности описывают движение водных потоков, возникающих в нижних бьефах дорожных дренажных систем, систем орошения, небольших мостов, каналов водоемов, различных водопропускных труб. Полученные зависимости распределения скоростей, глубины и геометрии потока воды дают большую точность, чем использованные ранее методы, как по значениям скорости, так и по геометрии граничных линий тока. Это позволяет рассчитывать параметры гидротехнических сооружений.
гидротехнические сооружения, двумерный бурный поток воды, трубы прямоугольного и круглого сечения, широкий горизонтальный отводящий канал, уравнения Эйлера, расчет скоростей и граничных линий тока
Целью настоящей работы является обзор различного вида уравнений движения двухмерного в плане открытого водного потока и решение некоторых практических задач с помощью этих уравнений.
Основные допущения и исходные физические предпосылки двухмерных в плане водных потоков следующие:
а) вертикальные (или нормальные к выбранной координатной плоскости) составляющие местных осреднённых скоростей и ускорений малы;
б) векторы скоростей жидких частиц, расположенных на одной вертикали, лежат в одной плоскости;
в) распределение скоростей на любой вертикали практически равномерное.
Можно выделить достаточно широкий класс потоков, параметры которых отвечают этим допущениям.
Такие потоки называют двухмерными в плане, отражая то, что для их описания достаточно двух геометрических координат x, y.
В широкой математической и технической литературе известно, что для постановки и решения различных прикладных задач по течению водных потоков необходимо пользоваться уравнениями движения, описывающими процесс течения жидкости, и знать начальные и граничные условия.
Так сложилось исторически, что основоположники теории двухмерных в плане водных потоков исходили из динамических уравнений движения идеального двухмерного открытого водного потока в форме Л. Эйлера (уравнений движения идеальной жидкости), дополненных слагаемыми, учитывающими силы сопротивления жидкости:
где X, Y, Z – компоненты объёмных сил; Tx, Ty, Tz – компоненты сил сопротивления, отнесённых к единице массы жидкости; r – плотность жидкости; p – местное давление; ux, uy, uz – компоненты вектора местной скорости.
Для установившегося потока при вертикальном направлении оси z и действии в жидкости единственной объёмной силы (силы тяжести) система (1) приобретает вид:
В силу посылки о малости вертикальных составляющих скоростей и ускорений все инерционные составляющие, содержащие uz и её производные, могут быть отброшены.
Тогда третье уравнение системы (2) примет вид:
где g – ускорение силы тяжести.
Интегрируя уравнение (3), получим:
где 
– произвольная функция.
С учётом того, что на свободной поверхности 
, приходим к гидростатическому закону распределения давлений на вертикали:
Обозначив через z0 координату дна водотока, получим:
Тогда систему динамических уравнений движения потока можно записать в виде:
Дополнив эту систему уравнений уравнением неразрывности потока:
получим следующую систему течения потока в виде:
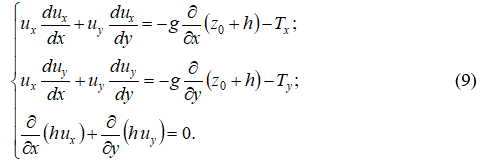
В частном случае, когда дно водовода горизонтальное, система (9) приобретает вид:
В ряде потоков, встречающихся в практике (выход потока из отверстия в расширение, вход потока в сужение, течение на виражах, на коротких участках) силами сопротивления потоку можно пренебречь, особенно в бурных высокоскоростных потоках, для которых силы инерции значительно превосходят силы тяжести, и система уравнений (10) приобретает вид:
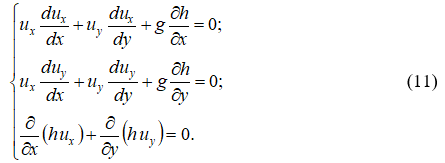
Система дифференциальных уравнений в частных производных (11) описывает течение двухмерных в плане открытых стационарных потоков в горизонтальном водоводе без учёта сил сопротивления потоку.
Эта система является системой существенно нелинейных уравнений, замкнутой относительно неизвестных функций:
С использованием системы (11) решаются различные задачи по течению двухмерных в плане водных потоков, как прямые, так и обратные.
Если ввести дополнительное условие потенциальности потока:
где W – вихрь для двухмерного потока, то существует потенциальная функция 
Система уравнений (11) в этом случае сводится к виду:
где H0 – постоянная для всего потока, определяемая по параметрам потока V0, h0 в некоторой характерной точке потока.
Первое конечное уравнение в системе (13) имеет название интеграла Д. Бернулли для двухмерных в плане водных потоков.
Система уравнений (13) сводится к одному уравнению второго порядка в частных производных относительно потенциальной функции 
Это уравнение по внешнему виду совпадает с уравнением для потенциала скорости плоского безвихревого газа, причём скорости звука соответствует волновая скорость C.
Из уравнения неразрывности потока (8) следует существование функции тока, удовлетворяющей условиям:
Поэтому систему (11) можно свести также к одному дифференциальному уравнению второго порядка в частных производных относительно функции тока 
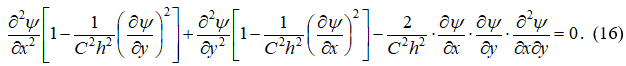
Уравнения (14), (16) служат исходными для разработки методов расчёта двухмерных в плане бурных потоков.
Для бурных потоков эти уравнения относятся к гиперболическому типу и для их исследования может быть использован метод характеристик.
К сожалению, метод расчёта потоков с использованием характеристик является численно-графо-аналитическим и даёт не всегда достаточную адекватность для практического пользования результатами модели.
Гораздо более точные результаты дают аналитические модели, изложенные в монографиях.
Следует заметить, что модель двухмерного в плане потенциального бурного потока, несмотря на значительную степень идеализации, имеет важное теоретическое и практическое значение.
Теоретическое значение заключается в том, что, исследуя простую модель, можно выявить характерные свойства потока и использовать их в более сложных моделях.
Практическое использование результатов модели потенциального течения в горизонтальном русле возможно в случаях, когда роль сил сопротивления относительно невелика (местные сужения, расширения или изгибы русла). В таких потоках основное формирующее влияние на параметры потока оказывает его инерционность и, если протяжённость потока незначительна, влиянием сил сопротивления можно пренебречь.
Аналитические методы решения различных задач по течению двухмерных в плане потенциальных потоков применяются:
а) в случае упрощений для потенциальной модели:
- уравнения движения простой центрированной волны;
- радиальный поток (безнапорный потенциальный источник).
б) при использовании вспомогательной плоскости годографа скорости.
Согласно уравнениям (13), (15) систему движений двухмерных в плане потенциальных водных потоков можно записать в виде:
Переходом в плоскость годографа скорости 
, в которой независимыми координатами являются 
(квадрат скоростного коэффициента) и угол q, характеризующий направление вектора скорости, уравнения (17) трансформируются к виду:
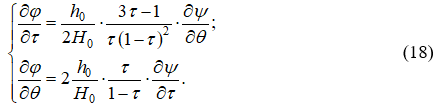
Формулы для определения глубин и скоростей при заданном параметре t имеют вид:
Зависимыми параметрами, неизвестными функциями в системе (18) являются 
– потенциальная функция; 
– функция тока, при этом для бурных потоков
Формулы (19) следуют из интеграла Бернулли и из выражения для параметра t.
Система уравнений (18) является уже линейной системой дифференциальных уравнений в частных производных в отличие от системы (11). Эта система сводится к решению следующего уравнения математической физики:
Это уравнение рядом замен приводится к гипергеометрическому уравнению с действительными коэффициентами, решения которого известны. Авторы работы на базе аналитических решений системы (18) развили метод, который может использоваться при решении различных задач по течению потенциальных двухмерных в плане открытых стационарных водных потоков.
Сначала решается граничная задача в плоскости годографа скорости.
Далее переход в физическую плоскость течения потока осуществляется использованием дифференциальной связью между планом течения потока и плоскостью годографа скорости:
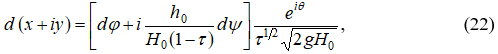
где 
– мнимая единица; x, y – координаты жидкой частицы потока в плане его течения; t, q – независимые координаты в плоскости годографа скорости; 
– потенциальная функция; 
– функция тока.
В работах авторы разработали детальную технологию решения задач по течению двухмерных в плане потенциальных потоков.
В работах приведены уравнения характеристик в плоскости годографа скорости; этот результат и аналогия внешнего вида уравнений совершенного газа и потенциального двухмерного в плане водного потока позволили авторам работ использовать преобразование С.А. Чаплыгина для получения системы (18) и разделения решения граничной задачи на два этапа:
1-й – решение задачи в плоскости годографа скорости;
2-й – получение алгоритма определения параметров потока в физической плоскости течения (в плане течения) с помощью интегрирования связи (22) при найденных на 1-м этапе функциях 
Далее приведём один из методов определения сил сопротивления потоку при использовании системы (9).
Для потоков, в которых нельзя пренебречь силами сопротивления потоку со стороны водовода, учёт сил сопротивления можно по предложению авторов в осуществить сведением поверхностных сил к некоторым эквивалентным объёмным.
Если t – касательное напряжение в основании элементарного цилиндрического объёма, то сила трения по дну равна 
. Направление вектора этой силы противоположно направлению вектора скорости 
Тогда абсолютные величины этой силы, отнесённые к единице массы выделенного объёма, выразятся формулами:
Или, вводя коэффициент гидравлического трения:
компоненты сил сопротивления переписываются в виде:
Как известно из, коэффициент Шези C связан с коэффициентом гидравлического трения соотношением:
причём 
; показатель y определяется конкретным законом сопротивления, приводимым в известной литературе по гидравлике; n – коэффициент шероховатости стенок водовода.
Для разрывных течений по параметрам потока пользуются двухмерными уравнениями планового потока (Сен-Венана), записанными в виде:
S – произвольная поверхность в пространстве (x, y, t), ограничивающая некоторый объём R в этом же пространстве; h – глубина потока; u, u – соответственно продольная и поперечная компоненты скорости; zn – отметка свободной поверхности потока; zд – отметка дна; l – коэффициент гидравлического трения; g – ускорение силы тяжести.
Для дифференцируемых функций, применяя к (26) теорему Гаусса – Остроградского, после некоторых преобразований получим уравнения Сен-Венана в дифференциальном виде:
Для стационарных потоков и для 
получим:
Эта система совпадает с точностью до обозначений компонент скорости с системой (11).
Приведём метод решения важной для практики задачи определения сопряжённых параметров струи двухмерного в плане бурного потока при её ударе о боковую стенку (рис. 1) на базе использования уравнений движения в интегральной форме.
Пусть в точке M до удара крайней линии потока о боковую стенку русла он имеет параметры V1, h1, q1.
Необходимо определить параметры потока в точке M после удара V2, h2 и угол d отклонения линии схода от боковой стенки русла.
Для определения величин V2, h2, d воспользуемся уравнением стационарного движения потока в интегральной форме без учёта сил сопротивления потоку:
Составляя алгоритмическую форму уравнения применительно к четырёхточечному шаблону 1M23 (см. рис. 1), две точки которого находятся на линии схода, и разрешая её относительно параметров потока в точке M, получим алгебраическую систему:
Так как до удара крайней линии тока о боковую стенку системе (30) должны удовлетворять параметры V1, h1, q1, то
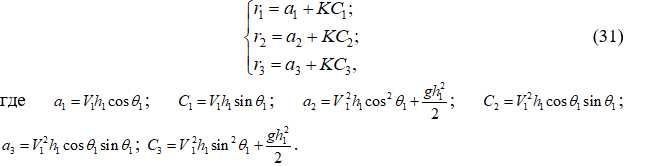
За прыжком в точке M угол 
и, следовательно, из системы (30) следует:
В системе (32) три неизвестных параметра V2, h2, K и для её совместности должно выполняться условие:
Определив из уравнения (33) неизвестное K, определим далее и сопряжённые параметры потока V2, h2, d за прыжком:
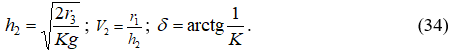
Ранее в литературе по гидравлическим расчётам для решения задачи определения параметров V2, h2, d необходимо было пользоваться громоздкими номограммами, имеющими ограничения 
, что сильно затрудняло получение достоверного результата.
Выводы. Исследователи в области моделирования течений двухмерных в плане открытых водных потоков могут воспользоваться уравнениями движения потока в зависимости от решаемой задачи в любой форме, изложенной в настоящей работе, и получить результаты моделирования с точностью, превышающей известную по ранее используемым методам. Особенно удобен метод расчёта потенциальных потоков с использованием плоскости годографа скорости.
1. Емцев Б.Т. Двухмерные бурные потоки. - М.: Энергия, 1967. - 212 с.
2. Высоцкий Л.И. Управление бурными потоками на водосбросах. - М.: Энергия, 1990. - 280 с.
3. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. - М.: Наука, 1970. - 720 с.
4. Арсенин В.Я. Методы математической физики и специальные функции. - М.: Наука, 1984. - 384 с.
5. Тихонов А.Н., Самарский А.А. Уравнения математической физики. - М.: Наука, 1986. - 106 с.
6. Есин А.И. Развитие теории и методов расчёта стационарных и нестационарных движений воды: Автореф. дисс. на соиск. уч. степ. д-ра техн. наук: 05.23.16. - М., 2004. - 48 с.
7. Есин А.И. Задачи технической механики жидкости в естественных координатах / ФГОУ ВПО «Саратовский ГАУ». - Саратов, 2003. - 144 с.
8. Чаплыгин С.А. Избранные труды / Механика жидкости и газа. Математика. Общая механика. - М.: Наука, 1976. - 496 с.
9. Коханенко В.Н., Волосухин Я.В. и др. Моделирование одномерных и двухмерных открытых водных потоков / НГМА; В.Н. Коханенко, Я.В. Волосухин, В.В. Ширяев, Н.В. Коханенко; под общ. ред. д-ра техн. наук, проф. В.Н. Коханенко. - Ростов н/Д: Изд-во ЮФУ, 2007. - 168 с.
10. Коханенко В.Н., Волосухин Я.В. и др. Моделирование бурных двухмерных в плане водных потоков: монография / В.Н. Коханенко, Я.В. Волосухин, М.А. Лемешко, Н.Г. Папченко; под общ. ред. д-ра техн. наук, проф. В.Н. Коханенко. - Ростов н/Д: Изд-во ЮФУ, 2013. - 180 с.
11. Ширяев В.В., Мицик М.Ф. и др. Развитие теории двухмерных открытых водных потоков: монография / В.В. Ширяев, М.Ф. Мицик, Е.В. Дуванская; под общ. ред. В.В. Ширяева. - Шахты: Изд-во ЮРГУЭС, 2007. - 133 с.
12. Штеренлихт Д.В. Гидравлика. / Изд. 3-е, перераб. - М.: Колос, 2005. - 656 с.
13. Справочник по гидравлике / Под ред. В.А. Большакова. Изд. 2-е, перераб. и доп. - К.: Вища школа, 1984. - 343 с.
14. Милитеев А.Н., Тогунова Н.П. Метод расчёта сопряжения бьефов в пространственных условиях / Гидравлика сооружений оросительных систем: тр. НИМИ. - Новочеркасск, 1976. - Т. 18. - Вып. 5. - С. 180-194.
15. Weiming Wu, M.ASCE Depth-Averaged Two-Dimensional Numerical Modeling of Unsteady Flow and Nonuniform Sediment Transport in Open Channels // Journal of Hydraulic Engineering Vol. 130, Issue 10 (October 2004) doi:https://doi.org/10.1061/(ASCE)0733-9429(2004)130:10(1013)
