В статье говорится об актуализации интегративной задачи в преподавании начертательной геометрии и ее роли в различных подходах в обучении. Методика введения в практику преподавания дисциплины интегративных задач позволяет реально и эффективно оценивать уровень сформированности прогнозируемых умений в начертательной геометрии.
начертательная геометрия, интегративная задача, подходы в обучении, умения
Вопрос эффективности обучения был, есть и, безусловно, всегда будет актуальным в педагогической практике. Существуют различные методики геометро-графической подготовки студентов, постоянно разрабатываются и внедряются новые [1, 2]. Главным критерием правомерности любой инновации является успешность ее результата [3]. Для объективной оценки уровня сформированности прогнозируемых умений необходим соответствующий инструментарий. В преподавании дисциплин графического цикла таким инструментарием является задача. Цель данной статьи – показать, какой должна быть учебная задача на определенном этапе обучения начертательной геометрии и о ее роли в контексте общего процесса научного познания [4].
Современная российская, а также зарубежная система образования широко используют различные подходы к организации педагогического процесса: системный, деятельностный, личностный, компетентностный, когнитивный, проблемный, развивающий и др. [5]. Термин «подход» в дидактике трактуется как сочетание принципов, определяющих стратегию обучения, когда каждый принцип корректирует разрешение возникающих в процессе обучения конкретных противоречий, а взаимодействие этих принципов приводит к разрешению основных противоречий образовательного процесса.
В данном исследовании не ставится цель подробного рассмотрения дидактики конкретных подходов, обозначенных выше. Все они показали неплохие результаты и положительно зарекомендовали себя. Предметом нашего изучения является такая задача, которая бы удовлетворяла содержанию самой дисциплины «Начертательная геометрия» и была релевантной одновременно каждому из наиболее известных в педагогической практике подходов [6].
Первый блок изучения начертательной геометрии включает: рассмотрение точки, прямой и плоскости, а также решение позиционных и метрических задач с перечисленными выше геометрическими объектами. Предполагаем, что хорошим логическим завершением изучения данного блока может стать интегративная задача, которую следует предложить студентам для решения.
Под интегративной задачей будем понимать функционал с определенным набором данных, соотносящихся друг с другом соответствующим образом и требованием ответа на поставленный вопрос, процедура решения которой предполагает естественную целостность познания объектов на основе установления связей и отношений между искусственно разделенными компонентами педагогического процесса, а также совокупность приемов и операций (включая их вариативность), приводящих к ответу на поставленный в задаче вопрос.
Предлагаем следующие критерии, определяющие интегративную задачу:
– в условии должны быть заданы более двух геометрических объектов;
– в вопросе желательно требование по одновременному выполнению более чем одного условия;
– задача должна иметь несколько решений;
– решение может быть выполнено в разных проекциях;
– в алгоритме не должны содержаться (либо использоваться по минимуму) однотипные действия;
– целесообразно, если содержание задачи имеет профессионально направленный контекст.
Далее рассмотрим пример такой задачи.
Задача. Даны три горных выработки: а, b, c. Требуется разработать горную выработку d, которая бы пересекала горные выработки a и b и проходила параллельно горной выработке с.
Первоначально необходимо переформулировать условие задачи с языка инженерной терминологии на язык начертательной геометрии. Для этого горные выработки как объекты, длина которых значительно превосходит размер их поперечного сечения, условно будем рассматривать как прямые. Таким образом, в терминологии изучаемой дисциплины задача получает новое прочтение: даны прямые а, b, c. Требуется провести прямую d, которая бы пересекала прямые a и b и проходила параллельно прямой с.
Покажем четыре способа решения данной задачи на разных геометрических моделях: в ортогональных проекциях на одной плоскости проекций (в проекциях с числовыми отметками), в ортогональных проекциях на двух плоскостях проекций, в ортогональных проекциях на нескольких взаимозаменяемых плоскостях проекций и в косоугольных проекциях. Графическое условие задачи и первый способ ее решения представлены на рис. 1.
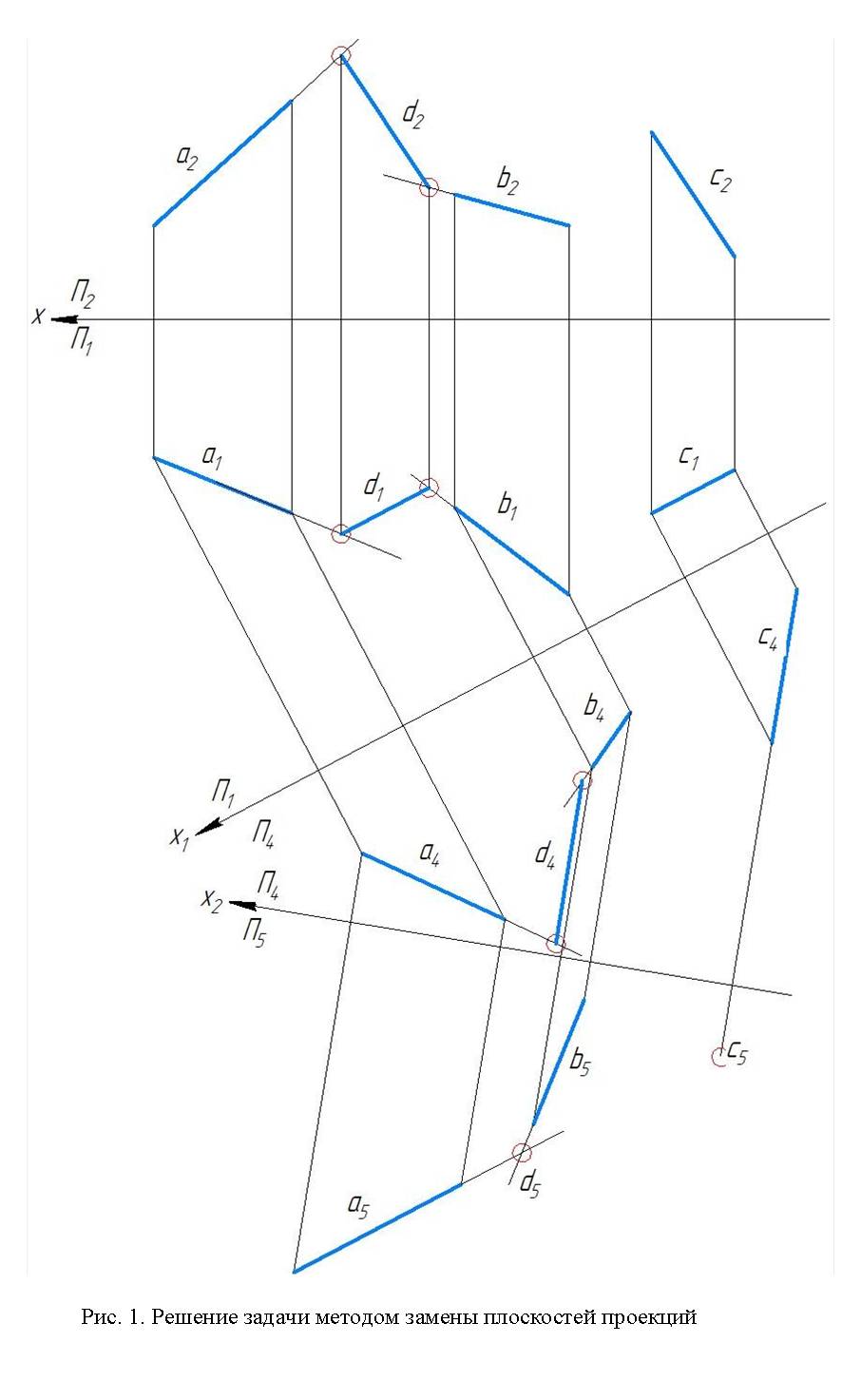
Сущность способа заключается в том, что при неизменном положении объекта в пространстве производится замена данной системы плоскостей проекций новой системой взаимно перпендикулярных плоскостей проекций. При переходе к новой системе одну из плоскостей проекций заменяют новой плоскостью таким образом, чтобы данный геометрический объект (в данном случае прямая) в новой системе занял частное положение и проецировался на одну из плоскостей без искажения. В данной задаче произведено две замены. При первой замене новая плоскость P4 расположена параллельно прямой c, при второй вновь введенная плоскость P5 перпендикулярна прямой с, поэтому она проецируется на эту плоскость в точку. Прямая d параллельна прямой c, следовательно, ее проекция также вырождается в точку. Так как прямая d должна пересекать прямые a и b, то ее вырожденная проекция находится на пересечении проекций прямых a и b.
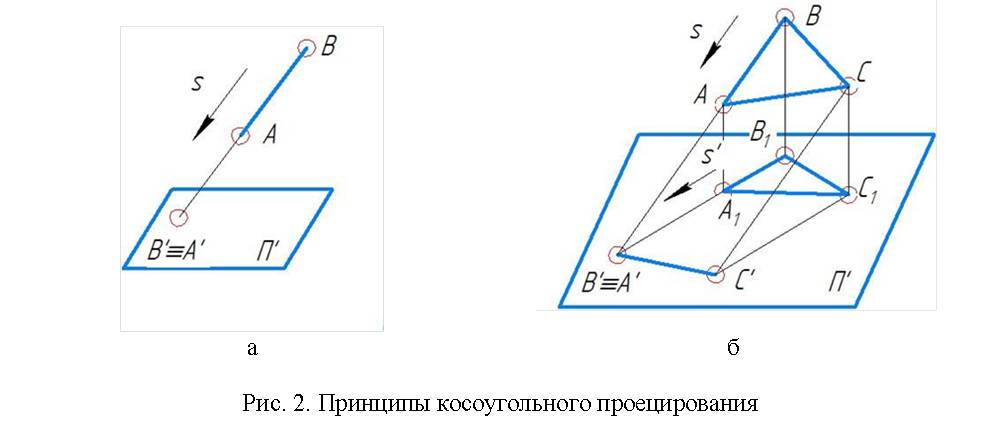
Рассмотрим второй способ решения задачи. Использование этого способа во многих случаях упрощает решение. Суть способа заключается в том, что применяется не традиционное прямоугольное, а косоугольное проецирование. Направление проецирования выбирается таким образом, чтобы получить вырожденную проекцию объекта. В результате теряется одно измерение. В частности, прямая проецируется в точку, а плоскость – в линию. Полученные результаты обратным проецированием переносятся на заданные проекции. Чтобы спроецировать прямую в точку, т.е. получить ее вырожденную проекцию, следует выбрать направление проецирования, параллельное прямой (рис. 2, а). Вырожденную проекцию плоскости можно получить, если направление проецирования будет параллельным плоскости (рис. 2, б).
Поскольку прямая должна удовлетворять трем условиям: пересекать прямую a; пересекать прямую b; быть параллельной прямой c, то множество прямых, отвечающих первому и третьему условиям, представляют собой плоскость S, определяемую прямыми a и l, причем l// c . Вторую плоскость W, которая определена прямыми b и m (m//c), образует также множество прямых, удовлетворяющих второму и третьему условиям задачи. Пересечение этих двух множеств прямых будут определять искомую прямую d. Таким образом, решается задача в косоугольных проекциях (рис. 3).
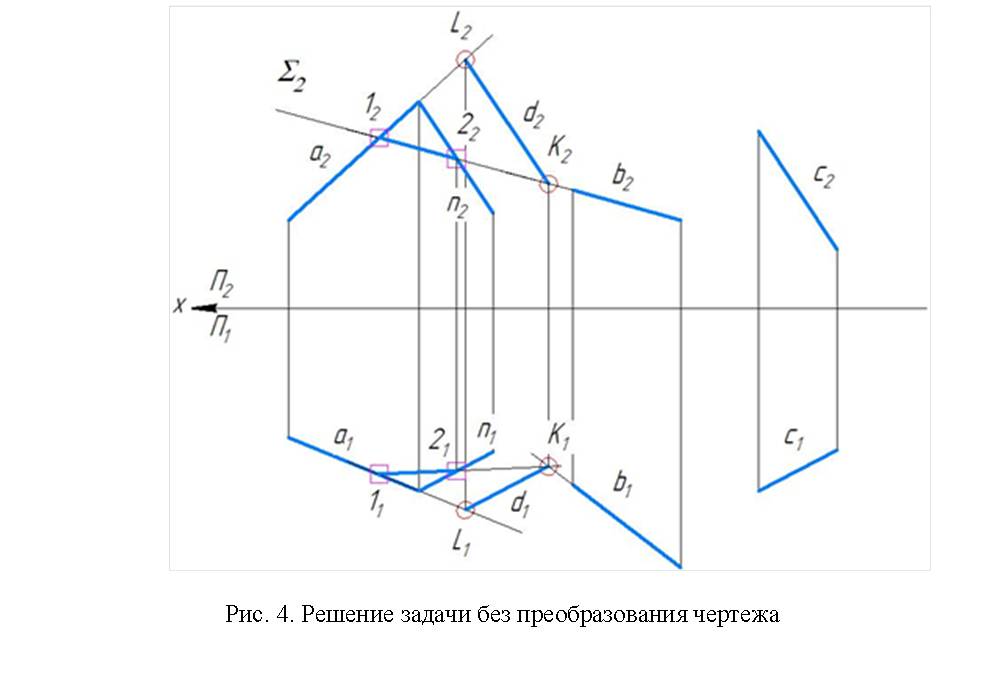
Третий способ решения задачи осуществим без преобразования чертежа (рис. 4). Проводим плоскость W параллельно прямой c (зададим ее двумя пересекающимися прямыми a и n, причем n параллельна c). Определяем точку K (пересечение прямой b с плоскостью W) и проводим через нее искомую прямую d параллельно прямым c и n и пересекающую прямую a в точке L.
Четвертым способом рассмотрим решение задачи в проекциях с числовыми отметками [7] (рис. 5). Через произвольную точку на прямой AB проводим прямую m,параллельную отрезку MN. Прямая mи отрезок AB определяют плоскость å, которую отрезок CD пересекает в точке K. Она находится с помощью плоскости − посредника. Через точку K проводится искомая прямая KL параллельно прямым m и MN.
Представив четыре способа графического решения задачи методами начертательной геометрии, проанализируем ее с точки зрения дидактики. Согласно определению, сформулированному выше, данная задача является интегративной, поскольку образует систему объектов, соотносящихся друг с другом определенным образом, между которыми установлены соответствующие связи. Так, в задаче рассматриваются во взаимодействии такие геометрические модели как точка, прямая и плоскость, а процесс решения складывается из совокупности различных приемов и операций [8, 9]:
– используются различные способы задания геометрических объектов на чертеже;
– для преобразования геометрических объектов применяется метод перемены плоскостей проекций;
– исследуется и устанавливается взаимное положение объектов;
– рассматриваются прямые и плоскости общего и частного положения;
– определяется натуральная величина прямой;
– выполняется преобразование прямой общего положения в линию уровня и проецирующую прямую;
– определяется точка пересечения прямой с плоскостью;
– рассматривается свойство параллельности прямых;
– в проекциях с числовыми отметками (ПЧО) вводятся понятия «интервал прямой», «интервал плоскости», «градуирование прямой», «градуирование плоскости»;
– в ПЧО определяется линия пересечения плоскостей.


Перечисленное и описанное выше позволяет утверждать, что данная задача удовлетворяет всем критериям интегративной задачи.
В связи с тем, что приемы и операции, которыми необходимо владеть студенту для успешного решения рассматриваемой задачи, включают в себя бо́льшую часть изучаемого материала первого блока дисциплины, то представленная интегративная задача может рассматриваться как функционал проверки уровня сформированности прогнозируемых умений в начертательной геометрии на определенном этапе обучения.
Кроме того, данная задача является релевантной и усиливает позиции таких известных подходов в обучении, как системного, деятельностного, исследовательского, контекстного, профессионально направленного, компетентностного, поискового, развивающего, личностно-ориентированного, что позволяет сфокусировать внимание на интегративных задачах в практике обучения студентов дисциплине «Начертательная геометрия». Решение интегративных задач развивает у студентов системное, пространственное и креативное и мышление, учит анализировать различные варианты решения задач и выбирать оптимальные.
1. Федосеева М.А. Методика подготовки студентов технических вузов графическим дисциплинам // Геометрия и графика. - 2019. -№ 1. -С. 68-73. - DOI:https://doi.org/10.12737/article_ 5c91fed8650bb7.79232969
2. Назарова О.Н. Современные проблемы преподавания курса «Прикладная геометрия и инженерная графика» для эксплуатационных направлений авиационного вуза // Геометрия и графика. - 2020. -Т. 8. -№ 2. -С. 58-65. - DOI:https://doi.org/10.12737/2308-4898-2020-58-65
3. Сальков Н.А. Качество геометрического образования при различных подходах к методике обучения // Геометрия и графика. - 2020. -Т. 8. -№ 4. -С. 47-60. - DOI:https://doi.org/10.12737/2308-4898-2021-8-4-47-60
4. Верещагина Т.А. Эволюционный процесс формирования умений решения инженерных задач // Инновации в образовании. -2013. - № 10. -С. 27-35.
5. Назарова О.Н. Адаптация дисциплины «Прикладная геометрия» к программамбакалавриата эксплуатационных направлений авиационного вуза // Геометрия и графика. -2020. -Т. 8. - №1. - С. 57-64. - DOI:https://doi.org/10.12737/2308-4898-2020-57-64
6. Верещагина Т.А. Роль инженерных задач в обучении моделированию горно-геологических объектов в процессе геометро-графической подготовки // Вестник Череповецкого государственного университета. - 2013. - № 1-2 (46).- С. 86-90.
7. Верещагина Т.А. Метод проекций с числовыми отметками в решении инженерных за-дач: учеб.-метод. пособие /Т.А. Верещагина, Л.В. Кочурова, И.А. Турицына. - Пермь: Изд-во Перм. нац. исслед. политехн. ун-та, 2016. - 105 с.
8. Верещагина Т.А. Контекстная профессионально ориентированная образовательная среда как средство геометро-графической подготовки специалистов горно-геологического профиля // Инновации в образовании. - 2012. - № 6. -С. 27-37.
9. Мусаева Т.В., Ураго А.А. Дополненная реальность в проведении занятий по инженерным техническим дисциплинам проектирования // Геометрия и графика. - 2021. -Т. 9. -№ 2. - С. 46-55. - DOI:https://doi.org/10.12737/2308-4898-2021-9-2-46-55






