Москва, г. Москва и Московская область, Россия
УДК 004.42 Программирование ЭВМ. Компьютерные программы
УДК 519.8 Исследование операций
УДК 531 Общая механика. Механика твердых тел
УДК 534 Механические колебания. Акустика
УДК 539.2 Свойства и структура молекулярных систем
УДК 539.6 Межмолекулярные силы
УДК 620.9 Общая энергетика
УДК 624.042 Расчет нагрузок и напряжений
УДК 624.044 Расчет деформаций
УДК 699.8 Мероприятия по защите зданий, сооружений и конструкций. Изоляционные работы. Противоаварийные мероприятия
Для материаловедения актуальной задачей является задача получения композиционных материалов, легких и других бетонов с требуемым комплексом физико-технических свойств. Решение данной задачи связано с изучением процессов самоорганизации, устойчивости и распада различных неравновесных систем, к которым можно отнести композиционные материалы и бетоны в виде капиллярно-поровых структур. Такая возможность представляется перспективной, если анализ и количественные описания диссипативных систем и структур бетонов производить с учетом теории фракталов и фрактальной размерности. В работе исследована структура пенобетона при различной кратности увеличения и уменьшения масштабирования. Обосновано положение о том, что структура пенобетонов состоит из пор подобных по форме, но различных по размерам. Следовательно, такая структура самоподобна на различных масштабных уровнях. Можно предположить, что материал пенобетона сформирован из пор, т.е. тонких стенок-перемычек, плотно упакованных, неупорядоченных полидисперсных пор. Но стенки пор имеют выраженное поверхностное строение с размерностью равной двум. Таким образом «на лицо» - неоднозначность в оценке материала с пористой структурой. С одной стороны, он имеет явно пространственное строение с размерностью равной трем. С другой стороны – это сложная система, представляющая собой тонкие стенки-перемычки пор. Альтернативное решение даёт размерность такой системы, находящаяся в интервале 2 … 3 и, следовательно, являющаяся дробной величиной. В работе даны оценки дробных размерностей компонентов пенобетона.
марка пенобетона по плотности, дисперсная система, каолесценция, пора, фрактал, дробная размерность, мера
Введение
Пористость пенобетонов, как композиционного материала особого рода, обусловлена наличием пор в цементном камне, пор в самом заполнителе, пор контактной зоны между цементным камнем и заполнителем, а также процессами воздухововлечения, обусловленных введением пены [1].

Рис. 1. Фото электронного микроскопа
фрактальной структуры капиллярно-порового пространства пенобетона
Удобно дифференцировать поры по их происхождению, т к. это дает возможность применения расчетного метода для определения объемов отдельных групп пор. Наиболее обстоятельная классификация пор по происхождению предложена Н.А. Мощанским [2]. Но, по этой классификации трудно установить связь между свойствами и характером пористости, т.к. происхождение пор не всегда определяет ее влияние на стойкость. Так, например, поры одной группы (тупиковые и сквозные капилляры) оказывают различное влияние на стойкость бетона, а поры разного происхождения - контракционные и микрокапилляры - могут быть одинаково, как пассивны, так и опасны при попеременном замораживании и оттаивании бетона [3,4,5].
Для бетонных и железобетонных конструкций, в соответствии со СНиП 2.03.01-84* предусматриваются легкие бетоны, предствыленные в Табл. 1.
Таблица1
Легкие бетоны для бетонных и железобетонных конструкций
|
№ пп |
Марка по плотности |
Классы легкого бетона |
|
1 |
D800, D900 |
В2,5; В3,5; В5; В7,5; |
|
2 |
D1000, D1100 |
В 2 ,5 ; В3,5; В5; В7,5; В10; В12,5; |
|
3 |
D1200, D1300 |
В2,5; В3,5; В5; В7,5; В10; В32,5; |
|
4 |
D1400, D1500 |
В3,5; В5; В7,5; BIO; В12,5; В15; В20; В25; В30; |
|
5 |
D1600, D1700 |
В5; В7,5; BIO; В12,5; В15; В20; В25; ВЗО; В35; |
|
6 |
D1800, D1900 |
BIO; В12,5; В15; В20; В25; ВЗО; В35; В40; |
|
7 |
D2000 |
В20; В25; ВЗО; В35; В40 |
Параметры плотности определяются характеристиками ингредиентов [6,7,8,9,10] и:
- учтены пропорциями составляющих раствора;
- учтены маркой используемого цемента;
- учтены составом воды;
- учтены зернистостью песка;
- учтены объемом жидкости в приготовленной смеси;
- учтены условиями и способом отвердевания раствора (естественно или с подогревом);
- учтены наличием добавок поверхностно активных веществ;
- учтены применением пенообразователя, формирующим структуру пен;
- не учтена фрактальность строения структуры бетона;
- не учтена фрактальность структура воздуха, как основного строительного материала капиллярно-пористой структуры бетона.
Методы исследований
Фракталы. Фракта́л — множество, обладающее свойством самоподобия (объект, в точности или приближённо совпадающий с частью себя самого, то есть целое имеет ту же форму, что и одна или более частей) [11,12]. В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность
Определение «фрактал» использовано нами не только в качестве математического термина. Фракталом может называться предмет, обладающий хотя бы одним из указанных ниже свойств:
- Обладает нетривиальной структурой во всех масштабах. В этом заключается его отличие от регулярных фигур (таких как окружность, эллипс, куб, график гладкой функции). Так, если рассмотреть небольшой фрагмент регулярной фигуры в очень крупном масштабе, то похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, то есть во всех масштабах сохраняется одинаково сложная структура;
- Является самоподобным или приближённо самоподобным;
- Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую размерность исследуемого объекта.
Представим фрактальные геометрические, алгебраические, стохастические определения элементов капиллярно поровой структуры пенобетона, выражаемые через понятия размер, мера и размерность.
Размер. Понятие «фрактала» напрямую связано с понятием «дробной размерности». Размер исследуемого предмета определяется «метрикой». Часто, размер малоинформативен, например, при ответе на вопрос: «Что больше, длина иди высота предмета?» Правильный ответ подразумевает уточнение, а что с чем сравнивается. Сравнение размеров может быть более информативным если предметы сравнения подобны друг другу.
Мера. Понятие «мера» используют для измерения объектов, но она измеряется не метрикой. Её главное свойство заключается в том, что - мера аддитивна. При слиянии двух объектов, мера суммы объектов равна сумме мер исходных предметов.
Для одномерных объектов мера пропорциональна размеру. Например, если сложить отрезки длиной 1см и 3см, «сложить» их вместе, то длина «суммарного» отрезка будет равна 4см (1+3=4 см), - априори.
А для не одномерных тел, мера вычисляется нами по правилам, которые подбираются так, чтобы мера сохраняла аддитивность. Например, если взять квадраты (двумерные объекты) со сторонами 3см и 4см и «сложить» их, т.е. объединить их вместе, то по аддитивным правилам сложатся площади выбранных квадратов, т.е. (9+16=25см²), а не их метрики сторон (3 см и 4 см). В результате поучится квадрат с метрикой стороны равной 5 см.

Рис. 2. Пример «Меры» — объединения многомерных объектов
Результаты исследований
Пены. Потенциал Гиббса[1]. В пенах заполненные газом ячейки разделены пленками дисперсионной среды. При этом форма многогранников непрерывно меняется в процессе диффузионного переноса газа и коалесценции[2]. В результате коалесценции происходит уменьшение степени дисперсности эмульсий, пен и аэрозолей вплоть до их расслоения на две фазы (жидкость- жидкость или жидкость - газ).

Рис. 3. Ячейки пены и пенобетона разделенные пленками дисперсионной среды и рёбрами «Плато-Гиббса»
В работе для расчетов дисперсности пены, ее гидропроводности, радиуса каналов Плато –Гиббса в качестве модельной ячейки использован пентагональный додекаэдр (рис. 2), или компактный четырнадцатигранник. Отметим, что в реальной пене среднее число пленок, окружающих ячейку, близко к 14.
Наблюдается то, что в каждом ребре многогранника сходятся три пленки, углы между которыми составляют 120º. Места стыка пленок (ребра многогранника) характеризуются утолщениями, образующими в поперечном сечении треугольник. Эти утолщения являются каналами «Плато-Гиббса»[3]. Четыре канала Плато-Гиббса сходятся в одной точке, образуя по всей пене одинаковые углы 109о 28’. Площадь поперечного сечения треугольного канала Плато-Гиббса определяется как
где r — средний радиус пузырьков в пене.
Дискуссия
Связность «меры» и «размера». Обозначим понятие «размерность» — «D», понятие «меры» — «M», понятие «размера» — «L». Построим суперпозицию из приведенных понятий:
Так для двухмерных тел (D=2) мерой (M) является площадь (S, S = L2), для трёхмерных тел (D=3, V = L3) — объём (V).
Следствие 1. Если исследуемый объект (фигуру) отмасштабировать, т.е. уменьшить в N раз, то она будет укладываться в исходной фигуре ND раз.
Следствие 2. Если при уменьшении размера объекта (фигуры) в N раз, получается то, что она укладывается в исходной n раз (то есть мера её уменьшилась в n раз), то размерность объекта определим, как:
Следствие 3. Как обобщить понятия длины, площади и объема? Предлагаем использовать ранее высказанное понятие «мера» (measure). И далее, - таким образом понятие «меры» возможно обобщить понятием «массы» предмета. Все ранее упомянутые предметы и фигуры состоят из веществ, характеристическим свойством которых является «масса». Дробная размерность напрямую связана с изменением массы предметов и фигур при их естественном или искусственном масштабировании.
Самоподобные фигуры дают понимание того, как сравнивать «массы[4]». Очевидно, что при уменьшении масштаба отрезка в 2 раза, «масса отрезка» также уменьшается в 2 раза. При уменьшении масштаба квадрата в 2 раза, масса квадрата синхронно уменьшается в 4 раза.
Уменьшая масштаб куба в 2 раза (а мы привели в начале работы показатели прочности и плотности бетонов, приходящиеся на один кубический метр бетонов, воспользовавшись «кубовой» формой представления топологии бетонов), то масса куба уменьшается в 8 раз. Размерность куба при этом сохранится и будет равна: [ D1 :=log(8), D1=0.903, D2 :=log(2), D2=0.301, D :=$\frac{D1}{D2}$, D=3. .[5]
Традиционно, подбор составов бетонов осуществлялся методом абсолютных объёмов, в основе которого лежит уравнение абсолютных объемов, составленное исходя из предположения, что: бетон сразу же после укладки и уплотнения находится в абсолютно плотном состоянии, а его объем складывается из суммы абсолютных объемов составляющих компонентов:
$1000=\frac{Ц}{ρ_ц}+\frac{В}{ρ_в}+\frac{П}{ρ_п}+\frac{Д}{ρ_д}$
где Ц, В, П, Д – расходы соответственно цемента, воды, песка, добавки [кг/м3]; ρ – их плотности [кг/л]; 1000 – объем бетона [л].
Но, данный подход не учитывает:
- фрактальность строения структуры бетона;
- фрактальность структура воздуха, как основного строительного материала капиллярно-пористой структуры и компонентов бетона.
Тогда, с учётом приведенных положений и представляя структуру одного кубического метра бетона дробной размерностью, т.е. фракталом, а также принимая во внимание то, что размер полного фрактала равен единице (=1), то мера, как аддитивная величина его компонентов равна сумме мер его частей:
Так, как и сам фрактал, и его части имеют одинаковую размерность (D), то можно выразить меры, через размеры компонентов:
Тогда, если фрактал, а в нашем понимании и в представленной логике рассуждений это один кубический метр бетона, - образован из N подобных элементов (компонентов бетона), с коэффициентами подобия
$1=k_1^D+k_2^D+ ... +k_n^D$
где k1,k2, … , kn — составляющие (структурные компоненты одного кубического метра бетона): цемент (k1), вода (k2), песок (k3), ПАВ (k4), минеральная добавка (k5) и т.п., и это уравнение должно являться основной формулой подбора состава бетонной методом абсолютных объёмов.
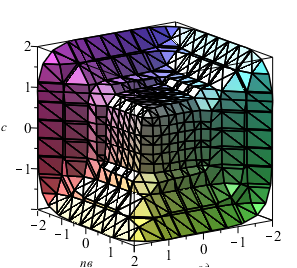
Рис.4. Графо-аналитическое представление одного кубического метра бетона
выражением абсолютных объёмов бетона дробной размерности «D»
c компонентами дробной размерности «D»
Аналитические выражения для определения расходов составляющих компонентов дробной размерности абсолютного фрактального объёма легкого бетона приобретают вид:
Пространство бетона размером в один метр кубический заполнено не в полной мере составляющими компонентами бетона, рис. 6.

Рис. 5. Заполнение «кубового» объёма бетона компонентами
(Цемент, Вода, Песок, ПАВ, Воздух) дробной размерности «D»
Обратим внимание на то, что, если все коэффициенты равны, то выражение превращается в:
Заключение
Вывод 1. Капиллярно-поровая структура пенобетона является фракталом, размерность которого можно парциально составляющим компонентам рассчитать.
Вывод 2. «Кубовый» объём легкого бетона заполнен формующим материалом не на 100%.
Вывод 3. Остаток незаполненного «кубового» объема пенобетона представляет собой объём вовлеченного воздуха, определяющий общий объём пор в одном метре кубическом пенобетона.
[1] Энергия Гиббса (или потенциал Гиббса, или изобарно-изотермический потенциал, или термодинамический потенциал в узком смысле) — это величина, изменение которой в ходе химической реакции равно изменению внутренней энергии системы. Энергия Гиббса показывает, какая часть от полной внутренней энергии системы может быть использована для химических превращений или получена в их результате в заданных условиях, и позволяет установить принципиальную возможность протекания химической реакции в заданных условиях.
[2] Коалесценция — слияние частиц (например, капель или пузырей) внутри подвижной среды (жидкости, газа) или на поверхности тела.
[3] (бельг.) Ж. Плато и (амер.) - Дж. Гиббс.
[4] Размерность треугольника «Серпинского» = log2(3) ≈ 1,585. Если масштаб уменьшается в 3 раза, «масса» уменьшается в 4 раза. Когда масштаб уменьшается в 3 раза, «масса» уменьшается в 4 раза. Тогда размерность кривой фон Коха = log3(4) ≈ 1,262 Уменьшая масштаб в 4 раза, «масса» уменьшится в 8 раз. Размерность = log4(8) ≈ 1,5
[5] Dкуба={[log2(8)] / [log2(2)]}=3
1. Дерягин Б.В. Упругие свойства тонких слоев воды. - Физическая химия, 1932, т. 3. - с. 18
2. Дерягин Б.В., Кусаков М.М.. - М.: Изд-во АН СССР. Серия химия, 1936, с - 46.
3. Мощанский Н.А., Плотность и стойкость бетонов. - М.: Госстройиздат, 1951. - 166 с.
4. Думанский А.В., Думанская А.П. Определение пористости гетеропорозных стенок. - Журнал физико-химического общества, 1939, вып. 3. - с. 67.
5. Стольников В.В. Исследование по гидротехническому бетону. - М.: Госэнегоиэдат, 1962. - 357 с.
6. Брилинг Р.Е. Воздухопроницаемость ограждающих конструкций и материалов. - М.: Стройиздат, 1948ю - 131 с.
7. Вербецкий Г.П. Структура и водонепроницаемость бетона. - в кн.: Труды совещания по теории технологии бетона. - Ереван, 1956. - с. 129.
8. Stull R.I. Johnson P.V. Ires. H.B.S., 1940, v. 25, p. 24.
9. Беркман А.С., Мельникова И.Г. Структура и морозостойкость строительных материалов. - М.: Л.: Госстройиздат, 1962. - 173 с.
10. Эдельман Л.И., Сомнинский Д.С., Копчикова Н.В. Исследование распределения пор по размерам в цементном каине. - Коллоидный журнал, 1961, №2 - с. 34.
11. Кравченко И.В., Юдович Б.Э. Опыт применения ртутной порометрии для определения дифференциальной пористости цементного камня. - Научные сообщения ВНИИЦемента, 1960, №9. - с. 90.
12. Бобрышев А.Н., Козомазов В.Н Бабин Л.О., Соломатов В.И. Синергетика композиционных материалов. - Липецк: НПО ОРИУС, 199462. - 151 с.


















